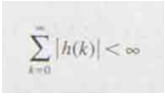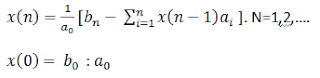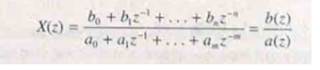Resume Bab4 deskripsi pole zero dalam sistem waktu diskrit
4.5.1 Pole-zero description of discrete-time systems.
Dalam kebanyakan sistem diskrit-waktu praktis, z-transform,
yaitu fungsi transfer sistem H (z), dapat diekspresikan dalam bentuk kutub dan
nol. Pertimbangkan, misalnya, z-transformasi berikut ini mewakili suatu filter
waktu-diskrit Nth-order umum (di mana N = M):

Dimana
The ak
and bk adalah koefisien dari filter. Jika H (z) memiliki
kutub pada z = p1, p2, ……., Pn dan nol pada z = z1, z2, ……., ZN, maka H (z)
dapat diperhitungkan dan diwakili sebagai.
4.5.2 Frequency Response Estimation
Ada banyak contoh
ketika diperlukan untuk mengevaluasi respon frekuensi sistem waktu diskrit.
Misalnya, dalam desain filter diskrit, seringkali perlu memeriksa spektrum
filter untuk memastikan bahwa spesifikasi yang diinginkan dipenuhi. Respons
frekuensi suatu sistem dapat dengan mudah diperoleh dari z-transformasinya.
Sebagai contoh,
jika kita menetapkan z = eiwT, yang mengevaluasi z-transform di
sekitar lingkaran unit, kita memperoleh transformasi Fourier dari sistem:
H (eiwT)
disebut sebagai respons frequencc dari sistem. Kami telah menggunakan simbol T
untuk menekankan ketergantungan respon frekuensi sistem diskrit-waktu pada
frekuensi sampling. Secara umum, H (eiwT) adalah kompleks.
Modulusnya memberikan respon besarnya dan fase respon fase dari sistem.
4.5.3 Geometric Evaluation of Frequency Response
Ini adalah metode
sederhana namun berguna untuk mendapatkan gambaran kasar tentang apa respon
frekuensi dari sistem diskrit-waktu akan terlihat, berdasarkan diagram
nol-kutubnya. Ingat bahwa z-transformasi sistem LTI dapat dinyatakan dalam
bentuk kutub dan nol:
Di mana kita
berasumsi, untuk kesederhanaan, bahwa perintah dari pembilang dan penyebut
adalah sama. Respon frekuensi diperoleh dengan membuat substitusi z = eiwT
dalam Persamaan 4.43 dan mengevaluasi H (eiwT) dalam interval ().
4.5.4 Direct Computer Evaluation of Frequency Response
Evaluasi geometrik
dari respons frekuensi memberi satu perasaan untuk respons frekuensi, tetapi
jelas sangat membosankan jika respons yang tepat diperlukan pada banyak
frekuensi. Meskipun prosesnya bisa otomatis, kesulitan menemukan lokasi kutub
dan nol membatasi kegunaannya.
4.5.5 Frequency Response Estimation Via FFT
FFT juga
dapat digunakan untuk mengevaluasi respon frekuensi sistem waktu diskrit. Cara
melakukan ini, untuk sistem IIR. Pertama-tama untuk mendapatkan respon impuls
dari sistem menggunakan, misalnya, metode rangkaian daya, dan kemudian
menghitung FFT dari respon impuls. Ini mengikuti langsung dari Persamaan 4.42b
yang menunjukkan bahwa respon frekuensi dari sistem diskrit-waktu hanyalah
Transformasi Fourier dari respon impulsnya. Untuk mendapatkan respons frekuensi
yang halus, penting untuk mengambil jumlah nilai respons impuls yang cukup dan
/ atau ke nol-pad nilai-nilai respon impuls sebelum FFT diambil. Bahasa C dan
implementasi MATLAB dibahas dalam lampiran.
4.5.6 Frequency Units Used in Discrete-time systems
Sistem atau
sinyal waktu kontinyu biasanya dijelaskan menggunakan Transformasi Laplace.
Dengan demikian respon frekuensi dari sistem waktu kontinu secara tradisional
dievaluasi dengan membiarkan s = jΩ dalam fungsi transfer sistem, H (s).
4.5.7 Stability
Considerations
Analisis
stabilitas sering dilakukan sebagai bagian dari desain sistem waktu diskrit.
Kriteria stabilitas yang berguna untuk sistem LTI adalah bahwa semua input yang
dibatasi menghasilkan keluaran yang dibatasi. Ini adalah apa yang disebut BIBO
(bounded input, bounded output) condition. Sistem LTI dikatakan stabil BIBO
jika dan hanya jika memenuhi kriteria.
Dimana h
(k) adalah respons impuls dari sistem. Jelas bahwa jika respon impuls adalah
panjang hingga kondisi di atas dipenuhi karena jumlah koefisien respon impuls
akan terbatas. Dengan demikian, pertimbangan stabilitas hanya berlaku untuk
sistem dengan respon impuls durasi yang tak terbatas.
4.5.8 Difference Equations
Persamaan
perbedaan menentukan operasi aktual yang harus dilakukan oleh sistem
diskrit-waktu pada data input, dalam domain waktu, untuk menghasilkan keluaran
yang diinginkan, persamaan perbedaan, untuk kebanyakan kasus praktis yang
menarik, dapat ditulis sebagai .
di
mana x (n) adalah sampel input, y (n) adalah sampel output, y (n - k) adalah
output sebelumnya dan ai, bk adalah koefisien sistem. Persamaan 3.54
menunjukkan bahwa output saat ini, y (n), diperoleh dari sampel input sekarang
dan yang lalu dan keluaran sebelumnya, y (n - k).
4.5.9 Impulse Response Estimation
Dalam
desain sistem waktu-diskrit, kebutuhan sering muncul untuk mendapatkan
nilai-nilai respon impuls. Sebagai contoh, dalam desain sistem FIR, respon
impuls diminta untuk menerapkan sistem, dan dalam desain sistem IIR nilai-nilai
diperlukan untuk analisis stabilitas. Respons impuls juga dapat digunakan untuk
mengevaluasi respons frekuensi sistem.
Respons
impuls dari sistem diskrit-waktu dapat didefinisikan sebagai inverse
z-transform dari fungsi transfer sistem, H (z)
4.5.10 Applications in Digital Filter Design
Salah satu
aplikasi terpenting dari z-transforrn di DSP adalah dalam desain dan analisis
kesalahan dalam filter digital, terutama filter IIR. Ini digunakan secara luas
untuk menentukan koefisien filter digital dan untuk menganalisis efek dari
berbagai kesalahan kuantisasi pada kinerja filter digital. Sebagai contoh,
sudah diketahui bahwa kesalahan kuantisasi adalah inheren dalam sistem
diskrit-waktu ketika mereka diimplementasikan dalam perangkat keras atau
perangkat lunak karena panjang register terbatas prosesor praktis.
Z-transformasi menyediakan cara yang nyaman untuk menganalisis efek dari
kesalahan tersebut pada kinerja sistem. Terutama, kesalahan karena pembulatan
atau pemotongan hasil dari operasi perkalian yang ditunjukkan dalam persamaan
perbedaan sering dianalisis dengan bantuan z-transform. Analisis kebisingan
dalam filter diskrit-waktu dibahas secara lebih rinci dalam Bab 13.
Aplikasi
penting lainnya dari z-transform dalam desain filter diskrit adalah
representasi dari struktur filter digital. Kami akan membahas ini secara lebih
rinci di sini karena ini memerlukan penggunaan program ekspansi fraksi parsial
yang disebutkan sebelumnya.
4.5.11 Realization structures for digital filters
Filter
waktu diskrit sering direpresentasikan dalam bentuk diagram blok atau aliran
sinyal. Diagram adalah cara mudah untuk merepresentasikan persamaan perbedaan
atau secara ekuivalen fungsi transfer. Pertimbangkan misalnya, filter diskrit
sederhana dengan persamaan perbedaan berikut:
Representasi
diagram blok persamaan ini ditunjukkan pada Gambar 4.14 (a). • Pada gambar,
simbol z-1 menunjukkan penundaan 1 unit waktu yang dapat dideduksi dari sinyal
pada berbagai node, panah mewakili pengganda dan konstanta di sampingnya faktor
perkalian. Hubungan antara persamaan perbedaan dan diagram blok harus jelas.
Representasi diagram alur sinyal persamaan perbedaan yang sama ditunjukkan pada
Gambar 4.14 (b). Adalah umum untuk merujuk pada blok atau diagram alir sebagai
diagram realisasi.
4.6 Summary
Pengetahuan
tentang z-transform sangat penting dalam pekerjaan DSP, karena merupakan alat
yang sangat berharga untuk mewakili, menganalisis dan merancang sistem waktu
diskrit. Kami telah menunjukkan cara mengevaluasi z-transformasi sekuens
waktu-diskret dan bagaimana memulihkan urutan dari z-transformasinya. Beberapa
program bahasa C disediakan untuk memungkinkan pembaca mendapatkan pemahaman
praktis tentang konsep dan aplikasi z-transform dalam pemrosesan sinyal.
Cobalah untuk menggunakannya kapan pun memungkinkan.
Appendices4A Recursive algorithm for the inverse z-transform
Dinyatakan
dalam teks utama bahwa metode pembagian panjang dapat disusun kembali dalam
bentuk rekursif. Secara khusus, kami ingin menunjukkan di sini bahwa diberi
z-transform, X (z), seperti itu
inverse
z-transform, x (n), dapat diperoleh sebagai (Juri, 1964)
4B C program for evaluating the inverse z-transform and for cascade-to-paralel struture conversion
Sebuah program bahasa C telah
dikembangkan untuk menghitung inverse z-transform menggunakan seri daya atau
metode ekspansi fraksi parsial. Program ini juga dapat digunakan untuk
membalikkan fungsi transfer sistem waktu diskrit, H (z), dari kaskade ke
struktur paralel. Program ini cukup besar dan karenanya untuk efisiensi diatur
ke dalam dua modul program, izt.c dan itilib.c, yang disimpan dalam file
terpisah, yang dapat dikompilasi secara terpisah dan kemudian dihubungkan:
Izt.c Program untuk menghitung inverse z-transform melalui rangkaian
daya atau ekspansi fraksi parsial, dan untuk mengkonversi dan untuk mengubah
fungsi transfer H (z) dalam bentuk kaskade ke fungsi transfer setara dalam
bentuk paralel melalui ekspansi fraksi parsial
Itilib.c perpustakaan fungsi termasuk fungsi power_series dan
partial_fraction.
4C C program for estimating frequency response
Program menghitung respons
frekuensi menggunakan metode estimasi langsung atau melalui FFf seperti yang
dijelaskan dalam Bagian 4.5.5. Transformasi-z dari sistem yang respons
frekuensinya diperkirakan harus dalam bentuk langsung atau kaskade. Sebuah
contoh akan memperjelas hal ini.
4D.1 Inverse z-t
Fungsi matlab kunci untuk
melakukan operasi z-transform inverse adalah deconv dan residuez. Fungsi dekonv
digunakan untuk melakukan pembagian panjang yang diperlukan dalam metode
penggunaan daya. Fungsi residu digunakan untuk menemukan koefisien fraksi
parsial dan kutub dari z-transform.
4D.1.1 Power series expansion with matlab
Dalam metode power series,
operasi kunci adalah divisi polinomyal. Matlab function deconv melakukan
operasi dekonvolusi. Dalam metode rangkaian daya, kami mengeksploitasi fakta
bahwa operasi dekonvolusi ekivalen dengan pembagian polinomial. Kemudian,
berikan z-transform, X (z), dari bentuk:
4D1.2 Partial fraction expansion with matlab
Matlab
fungsi residuez dapat digunakan untuk melakukan ekspansi fraksi parsial dari
z-transform, X (z), menyatakan rasio dua polinomial. Sintaks untuk perintah
residuez adalah
[r, p, k] =
residuez (b, a)
Dimana b
dan a adalah vektor yang mewakili pembilang dan denominator polinomial, b (z)
dan a (z), masing-masing dalam meningkatkan kekuatan negatif dari z sebagai
berikut
4D.3 Pole zero diagram
Matlab function
zplane, memungkinkan perhitungan dan tampilan diagram nol kutub. Sintaks untuk
perintahnya adalah
Zplane (b,a)
Dimana b
dan a adalah vektor koefisien dari pembilang dan denominator polinomial, b (z)
/ a (z). dalam format ini, perintah pertama menemukan lokasi nol polse (I, e,
akar b (z) dan a (z) masing-masing) dan kemudian plot z-plane diagram.
4D.4 Frequency response estimation
Toolbox
pemrosesan sinyal mengandung banyak fungsi berguna untuk menghitung dan
menampilkan respon frekuensi sistem diskrit-waktu. Yang paling banyak digunakan
adalah fungsi freqz. Berikan fungsi tranfer sistem dalam bentuk berikut:
Fungsi
freqz menggunakan pendekatan basis fft untuk menghitung respon frekuensi.
Fungsi ini memiliki berbagai format. Format yang berguna adalah [h, f] = freqz
(b, a, npt, Fa) di mana variabel b dan a adalah vektor dari pembilang dan
denominator polinomial. F0 adalah frekuensi sampling dan npt jumlah titik
frekuensi antara 0 dan F / 2 di toolbox matlab, frekuensi nyquist (I, e, F / 2)
adalah unit jika frekuensi dinormalisasi.
PENYUSUN :
 |
| Alfan Alfa |
 |
| Reza Syahrindra |
 |
| Woro Ayu |