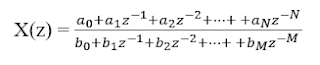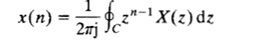Resume "bab 4" Transformasi-Z dan Penggunaan dalam Pemrosesan Sinyal
Sinyal Waktu-Diskrit dan Sistem
Sebuah sinyal diskrit
memiliki nilai-nilai yang didefinisikan hanya pada nilai-nilai diskrit waktu
atau beberapa
variabel lain yang sesuai, misalnya ruang. Sinyal seperti itu dapat dihasilkan
dengan sampling sinyal waktu kontinyu secara reguler dengan interval waktu
nT, n = 0, 1,
..., dimana T merupakan Periode Sampling. ini juga
bisa dihasilkan, dibuat, melalui beberapa algoritma pada komputer. Amplitudo dari
sinyal waktu-diskrit mungkin memiliki nilai diskrit (waktu diskrit, amplitudo
diskrit), atau mungkin bisa berkelanjutan. menurut kebiasaannya, sinyal waktu
diskrit direpresentasikan sebagai urutan angka.
x(n), n = 0, 1, ...
x(nT), n = 0, 1, ..
xn , n = 0, 1, ...
Dimana bentuk, x(n),
x (nT) atau xn menunjukkan
nilai sinyal dalam waktu diskrit n (atau nT).
Sistem waktu
diskrit pada dasarnya adalah algoritma dari matematika yang mengambil
urutan input, x (n), dan menghasilkan urutan
output, y (n). Contoh dari sistem
diskrit-waktu adalah pengendali digital, analisa spektrum digital, dan filter digital. Sistem waktu diskrit mungkin linier atau
nonlinier, waktu tidak bervariasi atau
waktu bervariasi. Sistem Linear time-invariant (LTI) membentuk kelas penting
pada sistem yang digunakan dalam DSP. Contohnya
adalah filter digital.
Sistem waktu-diskrit dikatakan linier jika memenuhi
prinsip-prinsip dari superposisi.
Yaitu, respons sistem linier terhadap dua input atau lebih, sama dengan jumlah tanggapan sistem terhadap setiap
input yang bertindak secara terpisah,dengan tidak adanya semua input lainnya.
Misal,
jika masukan, x1 (n), ke sistem memunculkan output, y1 (n), dan input lain x2 (n) maka menghasilkan output y2 (n), respon dari sistem untuk kedua input
akan
a1x1(n) + a2x2(n) ~ a1Y1(n) + a2y2(n) (3.2)
dimana
a1
dan a2
merupakan konstanta sembarang. Sistem diskrit waktu dapat dikatakan waktu invariant
(kadang-kadang disebut sebagai pergeseran
invariant) jika outputnya tidak bergantung pada waktu input diterapkan. Sebagai contoh, jika input x (n) memberikan output y
(n), maka input x (n - k) akan memberikan
output y (n - k):
x(n) y(n)
x(n - k) y(n - k)
ini merupakan delay yang
terjadi dalam input, menyebabkan penundaan dengan jumlah yang sama dalam output
sinyal. Hubungan input-output dari sistem LTI diberikan oleh
konvolusi jumlah.
y(n)=
dimana h(k) adalah respons impuls dari sistem. Nilai-nilai
h(k) sepenuhnya
mendefinisikan sistem waktu-diskrit dalam domain
waktu. Sistem LTI akan stabil jika respons impulsnya memenuhi kondisi.
Kondisi ini terpenuhi
jika h(k) memiliki durasi terbatas
atau jika h(k) meluruh
nol pada saat k bertambah. Sistem kausal adalah
sistem yang menghasilkan output hanya ketika ada masukkan. Semua sistem fisik adalah kausal. Secara umum,
urutan dari diskrit-waktu kausal, x(n), atau respon impuls, h(k), dari sistem diskrit-waktu adalah
nol
sebelum waktu 0, yaitu x(n) = 0, n <0, atau h(k)= 0, k <0.
Transformasi-Z
Transformasi-Z dari suatu
urutan,x(n), berlaku untuk semua n,
didefinisikan sebagai :
dimana z adalah variable kompleks
Di dalam
sistem kausal, x(n) mungkin bukan
hanya nol dalam interval 0 < n <
dan Persamaan 3.6 memperkecil ke yang disebut satu sisi z-transform:
Jelasnya,transformasi-z adalah rangkaian kekuatan dengan
bentuk nilai tak terbatas, sehingga mungkin tidak menyatu untuk semua nilai z.
Wilayah tempat dari transformasi-z
menyatu dikenal sebagai daerah dari persatuan
(ROC), dan di wilayah ini memiliki
nilai X(z)
terbatas.
Inversi Transformasi-Z
Sebuah inversi
transformasi-z (IZT) memungkinkan kita untuk memulihkan urutan diskrit-waktu,
x(n) cenderung
pada z-transformasinya. IZT sangat berguna dalam pekerjaan DSP,
contoh dalam menemukan respon impuls dari filter
digital. Secara simbolis, inversi
z-transformasi dapat didefinisikan sebagai :
dimana X(z) adalah z-transformasi dari x(n)
dan
adalah simbol untuk inversi dari
z-transform. Dengan
diasumsikan urutan dari kausal
z-transform, X(z) di dalam
Persamaan 3.7 dapat
diperluas menjadi rangkaian daya sebagai :
bahwa nilai x(n)
merupakan koefisien dari
(n = 0, 1, ...) dan bisa diperoleh langsung dengan inspeksi.
Dalam prakteknya, X (z) sering diekspresikan,
Tabel 4.1 Transformasi-z
dari beberapa urutan secara umum.
k dan
adalah konstanta; c adalah bilangan kompleks.
Rasio dua polinomial
dalam
atau ekuivalen di dalam z:
Di dalam bentuk ini, inversi dari transformasi-Z, x(n),
dapat diperoleh dengan menggunakan salah satu dari beberapa metode termasuk
tiga hal berikut:
1.
Metode
Perluasan Daya Seri
2.
Metode
Perluasan Fraksi Parsial
3.
Metode
Residu
Setiap
metode memiliki kelebihan dan kekurangannya sendiri. Di dalam hal ketelitian
matematis, metode residu mungkin yang sangat bagus. Metode daya seri,
bagaimanapun, paling mudah untuk peng-implementasian komputer.
Metode Daya Seri
Ditentukan
sebuah transformasi-Z,X(z),
dari urutan kausal seperti dalam Persamaan 3.11, itu dapat diperluas menjadi
deret tak terhingga di
atau z dengan pembagian panjang(terkadang
disebut pembagian sintetis) :
Di dalam metode ini, pembilang dan
penyebut dari X(z) pertama-tama
dinyatakan dalam kekuatan menurun keduanya dari z atau kekuatan naik dari
dan hasil baginya kemudian diperoleh dengan
pembagian panjang.
Metode Perluasan Sebagian Pecahan
Pada metode ini, transformasi-z, langkah pertama
diperluas menjadi jumlah pecahan sebagian secara sederhana. Inverse dari
transformasi-z masing-masing fraksi parsial kemudian diperoleh
dari tabel, seperti Tabel 3.1, dan kemudian
dijumlahkan untuk memberikan inverse keseluruhan dari transformasi-z. Dalam banyak kasus praktis,
transformasi-z diberikan sebagai perbandigan polinomial dalam z atau
dan memiliki bentuk yang sekarang dikenal:
Jika kutub
X(z) adalah urutan pertama dan N = M, maka X(z) dapat diperluas sebagai:
dimana
merupakan
kutub dari X(z) (diasumsikan berbeda),
adalah koofisien pecahan sebagian dan :
juga diketahui sebagai residu dari X(z); lihat
Bagian 4.3.3.
Jika urutan pembilang kurang dari penyebut dalam
Persamaan 3.14, yaitu N < M, maka
akan menjadi nol. Jika N> M maka X(z) harus
dikurangi pertama, untuk membuat N
M, dengan pembagian panjang pembilang dan
penyebut polinomial yang ditulis didalam daya
menurun dari
.
Sebagai pengingat dapat dinyatakan dalam Persamaan 3.15.
Koefisien dari
yang terkait pada tiang
dapat diperoleh dengan
mengalikan kedua sisi dari Persamaan 3.15 oleh (z
-
)
/ z dan kemudian melepaskan z =
:
Jika X(z) berisi satu atau
lebih banyak orde kutub (yaitu kutub-kutub yang bertepatan) maka persyaratan
tambahan diperlukan dalam Persamaan 3.15 untuk mengambil ini menjadi
sebuah perhitungan. Sebagai contoh, jika X(z)
berisi orde tiang mth pada z =
parsial
ekspansi fraksi harus mencakup syarat-syarat dari
bentuknya :
Sebuah
koofisien,
,
dapat diperoleh dari
hubungan :
Metode Residu
Dalam metode
ini IZT diperoleh dengan menaksir garis dari integral
dimana C merupakan jalur integrasi yang
melingkupi semua kutub dari X(z). Untuk perbandingan
polinomial, garis integral pada Persamaan 3.28
ditaksir menggunakan fundamental yang menghasilkan
teori variabel kompleks yang dikenal sebagai teorema residu Cauchy (Mathews, 1982):
= penjumlahan residu dari
X(z) pada semua kutub didalam C.
Pada bagian
terakhir, dimulai dalam koefisien dari pecahan parsial,
juga bisa
disebut sebagai residu X(z) dan dengan cara mencatat nilai yang diberikan. Kunci
utama untuk diingat bahwa setiap residu,
dikaitkan
dengan kutub,
· Dalam metode
ini, residu dari
X (z) pada
kutub
(tidak residu
dari X(z)) ditentukan oleh :
dimana F(z) =
X
(z), m merupakan tatanan kutub pada
dan Res [F(z),
]
merupakan residu F(z) pada z =
· Contoh sederhana ( berbeda) kutub, Persamaan
3.30 mengurangi
menjadi :
Perbandingan metode inversi z -
transformasi
Kami
telah membahas secara rinci tiga metode untuk memperoleh inverse ztransformasi:
seri daya, ekspansi fraksi parsial dan metode residu. Batasan metode rangkaian
daya adalah bahwa ia tidak mengarah ke solusi bentuk tertutup (meskipun ini
dapat disimpulkan dalam kasus sederhana), tetapi sederhana dan cocok untuk
implementasi komputer.
Properti dari z - transform
Beberapa sifat yang berguna dari z-transform yang telah menemukan penggunaan praktis dalam DSP
dijelaskan secara singkat di bawah ini.
Bukti untuk beberapa properti ini diberikan sebagai masalah pada akhir bab ini.
1. Linearitas. Jika urutan X1 (n) memiliki z - transformasi X1 (z) dan X2 (z)
maka z - transform dari kombinasi liniernya adalah
Beberapa aplikasi z - mentransformasikan dalam pemrosesan sinyal
Aplikasi z-transform di DSP banyak. Beberapa di antaranya didiskusikan secara lebih rinci dalam
bab-bab selanjutnya, terutama di Bab 8. Beberapa bagian berikutnya dimaksudkan untuk menyoroti
beberapa aplikasi ini dan untuk menetapkan beberapa masalah mendasar yang umum bagi mereka.
 |
| Ahmad Ilham Dado |
 |
| Risa Febri |
 |
| Amin Rodhi |
pemrosesan sinyal digital, analog to digital converter circuit, analog to digital converter block diagram, analog to digital converter theory, pengolahan sinyal digital dengan pemrograman matlab pdf, digital signal processing, digital signal processing adalah, digital signal processing pdf, digital signal processing book, digital signal processing ppt, digital signal processing proakis, digital signal processing applications, pemrosesan sinyal digital pdf, pemrosesan sinyal digital adalah, pemrosesan sinyal digital john g proakis, pengolahan sinyal digital, pengolahan sinyal digital dengan pemrograman matlab, pengolahan sinyal digital pdf, pengolahan sinyal digital ebook, pengolahan sinyal digital ppt, rumus impuls, analog adalah, pengertian resolusi, pengertian pengolahan, digital adalah, pengertian konversi, pengertian transformasi, politeknik jambi, apa yang dimaksud dengan software, adc adalah, modulasi, fungsi radio, pengertian plc, pengertian mikrokontroler, data diskrit, materi transformasi, apa yang dimaksud dengan pengolahan, transformasi fourier, makalah gelombang elektromagnetik, diskrit, contoh soal pencerminan dan jawabannya, sinyal analog, definisi software, pengertian input dan output, perbedaan sinyal analog dan digital, perbedaan analog dan digital, pengertian analog, arti noise, sinyal adalah, converter adalah, jenis jenis sampel, makalah teknologi digital, pengertian bit, teknologi digital fisika, contoh data diskrit, sinyal 3, pengertian komunikasi digital, fungsi e learning, sinyal digital, modulasi digital, materi teknik elektro, pengertian sinyal, pengertian filter, mata kuliah teknik elektro, sinyal analog dan digital, tabel transformasi laplace, jenis mikrokontroler, pengertian a, sdr adalah, sinyal tri, apa itu converter, contoh soal bilangan kompleks dan penyelesaiannya, pengertian counter, contoh diktat, jelaskan perbedaan fungsi pertahanan dengan fungsi keamanan, jenis jenis mikrokontroler, materi elektronika dasar, dr aulia malang, macam macam sampling, contoh data kontinu, jenis jenis sampling, data kontinu, perbedaan am dan fm, modifikasi mixer 8 potensio, pengertian matlab, jenis jenis ic, contoh soal c1 c2 c3 c4 c5 c6, pengertian op amp, pengertian teknik elektro, contoh soal pencerminan, contoh soal deret fourier, deret fourier pdf, sinyal analog adalah, pengertian converter, fungsi converter, data diskrit dan kontinu, keluaran kr, pengolahan sinyal digital, utama audio, pengertian scada, jenis ic, cuplik, pengertian eigrp, kepanjangan adc, contoh pengolahan, contoh impuls dalam kehidupan sehari hari, sinyal digital dan analog, prinsip kerja op amp, aplikasi len, pengertian adc, makalah tentang gelombang elektromagnetik, pengertian pwm, merakit mixer 8 potensio, definisi radio, materi sistem digital, pengertian data diskrit, pengertian sistem digital, sinyal dan sistem, jenis jenis op amp, sinyal analog dan sinyal digital, arti adc, sinyal diskrit, frekuensi digital, mikrokontroler atmega16, kuliah teknik elektro, contoh soal deret fourier dan penyelesaiannya, prinsip kerja potensiometer, makalah tentang gelombang, definisi pengolahan, rangkaian adc, pengertian gambar digital, data analog, rumus frekuensi dan amplitudo, contoh sinyal analog, invers transformasi laplace, rumus adc, contoh soal op amp, konsep pengolahan audio, jenis ic dan fungsinya, contoh pencerminan, transformasi fourier pdf, jurnal akuisisi, apa yang dimaksud dengan filter, arti converter, sinyal data, perangkat pemroses, teknik pengolahan audio, rangkaian mixer 7 potensio, rangkaian band pass filter, adc dan dac, cara kerja multiplexer, pengertian analog dan digital, pengertian sinyal digital, perbedaan sistem analog dan digital, sistem digital pdf, rumus besar impuls, contoh soal komunikasi data, contoh aplikasi komunikasi data, sistem dinamis, definisi sinyal, gambarkan dengan model blok sistem kerja perangkat komputer, gambar counter, fungsi komparator, arti sinyal, data analog adalah, komponen digital, frekuensi cut off, converter waktu, pemrosesan sinyal digital, pengolahan sinyal, sinyal sinusoidal, pengertian low pass filter, pengertian sinyal analog dan digital, pengertian dac, materi scada, macam macam e learning, prinsip kerja adc, rangkaian low pass filter pasif, makalah gelombang elektromagnetik pdf, irwan kurniawan, contoh sinyal analog dan digital, prinsip kerja dac, transformasi laplace invers, analog to digital converter adalah, apa yang dimaksud dengan multiplexer, contoh sistem digital, fungsi adc, jenis jenis adc, prinsip kerja ic, pengertian komparator, alat yang mengubah sinyal analog menjadi digital atau sebaliknya adalah, cara menggambar tubuh manusia secara proporsional, contoh data digital, cara membuat blok diagram, contoh soal transformasi fourier, pengolahan sinyal digital pdf, data analog dan data digital, definisi broadcasting, contoh sensor analog, transmisi digital, pengertian audio digital, modul matlab, pengertian band pass filter, contoh soal penerapan matriks dalam kehidupan sehari hari, pengertian adc dan dac, macam macam ic op amp, materi kuliah teknik elektro, pengertian data digital, e learning itn, pengertian high pass filter, jenis jenis ic dan fungsinya, cara kerja adc, makalah tentang elektromagnetik, contoh aplikasi pengolah data, pengertian ramp, konversi analog ke digital, transmisi data analog dan digital, perbedaan data analog dan data digital, materi dasar elektronika, aplikasi transformasi laplace, cara kerja low pass filter, elektronika analog pdf, contoh rangkaian digital, rangkaian multiplexer dan contohnya, contoh analog dan digital, pengolahan audio, perbedaan alat ukur analog dan digital, contoh conversion, contoh soal refleksi terhadap sumbu y, sinyal x, pengertian elektronika daya, rumus low pass filter, kegunaan mikrokontroler, filter aktif pdf, sifat transformasi laplace, cara kerja emg, filter fir adalah, frekuensi gitar, contoh format bahan ajar, contoh data analog, filter iir adalah, pengertian folding, nilai angka digital dan bit adalah, sensor analog adalah, blok diagram sistem, aplikasi scada, fungsi dari e learning, makalah sistem digital, rangkaian converter, gambar komputer analog, pengertian conversion, rangkaian digital sederhana, fungsi low pass filter, silabus komunikasi data, materi teknik listrik, mata sensor ac, elearning itn, rangkaian komparator op amp, pengertian wireless sensor network, sistem analog dan digital, gambar novita, pengertian ladder diagram, pengertian fpga, konversi sinyal analog ke digital, rumus high pass filter, perbedaan data analog dan digital, aplikasi pengolah suara, frekuensi senar gitar, pengertian rangkaian digital, proses perubahan sinyal analog ke digital, komputer analog dan digital, cara kerja sinyal, contoh processing, definisi analog, pengertian konversi data, jenis jenis konverter, contoh gambar pencerminan, perbedaan adc dan dac, contoh soal sistem digital, contoh simulasi digital dalam kehidupan sehari hari, pengolahan sinyal digital ebook, sinyal audio, teknik komunikasi data digital, modul sampling, contoh soal transformasi laplace invers, contoh aplikasi rangkaian op amp, pengertian komputer menurut fuori, makalah transformasi laplace, materi elektronika analog, makalah ic, elektronika analog dan digital, pengertian audio analog, materi teknik pengolahan audio, contoh sistem analog, contoh aplikasi mikrokontroler, pengertian elektronika analog, pengertian optocoupler, sinyal fm, rangkaian digital pdf, pengertian frekuensi cut off, modul sistem digital, frekuensi cut off low pass filter, e learning itn malang, rangkaian mikrokontroler sederhana, rangkaian modulator am, materi deret fourier, contoh aplikasi sistem digital, rpp komunikasi data, analog ke digital, pengertian simulasi digital dan contohnya, aplikasi transformasi fourier, soal sistem digital, analog digital converter adalah, makalah modulasi digital, transformasi z pdf, komponen it, contoh block diagram, mengubah sinyal analog menjadi digital, jenis jenis rangkaian, modulasi fasa, pengertian signal generator, konverter analog ke digital, membuat amperemeter digital, soal dan jawaban menerapkan teknik elektronika analog dan digital dasar, jenis ic op amp, transformasi 2d, jenis ic digital, pengolahan sinyal digital dengan pemrograman matlab, sebutkan penggolongan macam macam perangkat lunak aplikasi, pengertian band stop filter, aplikasi pengolahan sinyal digital, rangkaian analog to digital converter, pengertian video analog dan digital, pengertian emg, pengertian timing diagram, aplikasi adc, pengertian teknik elektronika industri, fungsi mpeg, sistem digital dan analog, fungsi high pass filter, contoh soal dan pembahasan transformasi laplace, rumus daya akustik, pengantar komunikasi data, makalah dasar sistem kontrol, kelebihan dan kekurangan simulasi digital, contoh soal dimensi 2, materi dasar plc, pengertian dsp, pengertian analog to digital converter, contoh alat digital, pengertian sistem analog, pengertian sistem embedded, contoh aplikasi matlab, sistem kendali kontinyu, buku pengolahan sinyal digital, modulasi phasa, skema audio mixer 7 potensio, penguat sinyal radio am, maksud digital, pengertian audio analog dan audio digital, contoh soal dimensi 3 dan penyelesaiannya, audio utama, kelebihan dan kekurangan komputer analog, rangkaian adc 0804, makalah sistem pneumatik dan hidrolik, cara membuat h shifter, komponen delphi 7, membuat grafik pada matlab, pengertian digital to analog converter, jenis jenis mikrokontroler beserta gambarnya, makalah pneumatik hidrolik, proses konversi analog ke digital, apa yang dimaksud materi digital, materi register teknik digital, aplikasi elektronika digital, skema rangkaian mixer 7 potensio, soal menerapkan teknik elektronika analog dan digital dasar, materi elektronika analog dan digital dasar, soal elektronika digital, aplikasi rangkaian digital, keunggulan sistem digital, sistem telekomunikasi digital, rpp menerapkan teknik elektronika analog dan digital dasar, definisi plc secara umum, sifat sifat dari sistem komputer, contoh timing diagram, pembagian perangkat lunak secara garis besar, contoh makalah sistem digital, pengertian hamming code, makalah elektronika analog, materi audio digital, dimensi tiga matematika ppt, perbedaan audio digital dan analog, pengertian vhdl, buku sinyal dan sistem, fungsi rangkaian komparator, fungsi audio converter, sirkuit digital, sensor suara analog, alat untuk mengukur diameter senar gitar,