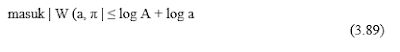Resume Bab 3 Discrete Transforms (3.7-3.10)
3.7 Pelaksanaan FFT
Pada
dasarnya harus jelas sekarang bahwa pada prinsipnya FFT atau IFFT dihitung
dengan menyediakan array data dan operasi pada data menggunakan FFT atau
algoritma IFFT (termasuk algoritma bit reversal).
3.7.1 Penipisan-in-frekuensi FFT
Algoritma
yang dihasilkan penipisan-in-frekuensi pertama kali diturunkan oleh Gentleman
dan Sande (1966) dan sering dikenal sebagai algoritma Sande-Tukey, sayangnya
untuk Gentleman. Secara keseluruhan ada sedikit untuk memilih antara dua
algoritma.
3.7.2
Perbandingan DIT dan DIF
algoritma
Untuk
algoritma DIF urutan input data tidak berubah namun output FFT urutan adalah
sedikit terbalik. Kedua DIF dan DIT algoritma algoritma di-tempat.
3.7.3
Modifikasi untuk
meningkatkan kecepatan
Kenaikan
lebih lanjut dalam kecepatan komputasi yang mungkin untuk algoritma DIT.
Sebagai contoh. radix-4 FFT dapat digunakan
untuk mengurangi jumlah perkalian kompleks dengan faktor mendekati 2. Jumlah
penambahan juga berkurang. peningkatan lain dalam kecepatan dapat diperoleh
dengan menghapus perkalian yang tidak perlu oleh WN faktor bobot (sering
disebut faktor bermalas!) yang terjadi ketika WN = ± 1, atau ± j. Hal ini juga
mengurangi jumlah penambahan diperlukan. Implementasi adalah dengan termasuk
kupu-kupu yang terpisah untuk kasus-kasus yang WN = ± 1, atau ± j. Ini,
misalnya, akan memberikan radix-2, dua-kupu-kupu, di tempat, algoritma DIT.
Selanjutnya penghematan waktu dapat diperoleh dengan terlebih dahulu menghitung
sinus dan cosinus bagian dari WN dan menyimpannya dalam tabel look-up dari mana
nilai-nilai mereka diperoleh seperti yang diperlukan.
3.8 Diskrit Lain
Transformasi
Berbagai
transformasi lain yang tersedia. The Winograd Fourier transform (Winograd 1978; lihat juga Burrus dan Taman, 1985; Beauchamp. 1987;
Rader, 1968; Komite Pengolahan sinyal. 1979; McClellan
dan Rader. 1979) dan algoritma faktor utama
(Beauchamp, 1987; lihat juga McClellan dan
Rader. 1979) memberikan ingenious tetapi metode rumit meningkatkan kecepatan
perhitungan FFT. The discrete cosine transform sangat useful
dalam aplikasi kompresi data (lihat Bagian 3.8.1). Transformasi Walsh (Bagian
3.8.2) menganalisa sinyal ke bentuk gelombang persegi panjang daripada yang
sinusoidal dan dihitung lebih cepat daripada FFT. The Hadamard transform
(Bagian 3.8.3). menipustructed dengan re-memerintahkan Walsh
memerintahkan urutan. bahkan lebih cepat
untuk menghitung. Sementara menampilkan keuntungan untuk beberapa tujuan Walsh
dan Hadamard transformasi menderita beberapa kelemahan yang membatasi
penerapannya; lihat Bagian 3.8.2 dan 3.8.3.
Akhirnya. Haar transformasi ini sangat
berguna untuk deteksi tepi dalam pengolahan citra (Rosenfield dan Thurston,
1971) dan untuk aplikasi yang serupa. Beauchamp (1987) menyediakan sumber yang
baik dari bahan awal bagi mereka yang ingin tahu lebih banyak tentang berbagai
transformasi dibahas dan aplikasi mereka. Selama tahun 1990-an ada minat yang
tumbuh di wavelet transform (Chan, 1995, Daubechies, 1990, 1992, Burns,
Gopinath dan Guo, 1998) dan sehingga memperkenalkan bawah dalam Bagian 3.8.4.
3.8.1
Discrete Cosine Transform
Tiga fitur penting dari yang cocok transformasi adalah efisiensi
kompresi, yang berkaitan dengan berkonsentrasi energi pada frekuensi rendah,
kemudahan perhitungan. dan minimum mean square error. yang ideal transformasi untuk
mencapai ini adalah Karhunerr-Loeve Transform. tapi
ini tidak dapat diwakili algorithmically. Namun,
discrete cosine transform (DCT) memiliki hampir sifat yang sama dan tidak
memiliki algoritma. Ini pada dasarnya terdiri dari bagian nyata dari DFT.
Definisi ini wajar sejak seri Fourier dari nyata dan bahkan Fungsi
hanya berisi istilah cosinus. dan dalam, misalnya. kasus tegangan
sampel nilai data yang digunakan adalah nyata dan dapat dibuat simetris dengan menggandakan
data dengan menambahkan bayangannya. Dengan
demikian DPT diberikan oleh (Persamaan 3.41)
Mendefinisikan DCT X c (k) sebagai
bagian nyata dari ini memberikan
Ini adalah salah
satu dari beberapa bentuk dari DCT. Bentuk yang lebih umum adalah (Beauchamp,
1987; Yip dan Ramamohan, 1987; Ahmed dan
Rao, 1975)
dan dua bentuk
lain juga ada (Yip dan Ramamohan, 1987).
Implementasi
dari DCT ada berdasarkan FFT seperti yang diharapkan (Narasinka dan Petersen,
1978), dan DCT cepat yang enam kali lebih cepat seperti ini telah dikembangkan
(Chen et al., 1977). Versi lain adalah C-matriks transformasi yang dapat lebih
sederhana dibangun di hardware (Srinivassan dan Rao, 1983).
3.8.2 Transformasi Walsh
Transformasi
yang dibahas sejauh ini telah didasarkan pada kosinus dan fungsi sinus.
Mentransformasi berdasarkan bentuk gelombang pulsa seperti yang mengambil hanya
nilai-nilai ± 1 yang lebih sederhana dan lebih cepat untuk menghitung. Mereka
juga lebih tepat untuk representasi dari bentuk gelombang yang mengandung
diskontinuitas, misalnya dalam gambar.
Sama
seperti DFT didasarkan pada satu set kosinus harmonis terkait dan bentuk
gelombang sinus, sehingga adalah diskrit transformasi Walsh (DWT) berdasarkan
satu set bentuk gelombang persegi panjang harmonis terkait. dikenal sebagai fungsi Walsh. Namun. frekuensi
tidak didefinisikan untuk bentuk gelombang persegi panjang dan begitu analogou
yangs sequency istilah yang digunakan.
Sequency adalah setengah jumlah rata-rata nol penyeberangan per satuan waktu.
Gambar 3.6 menunjukkan set fungsi Walsh hingga urutan N = 8 ditarik dalam
rangka peningkatan sequency. Mereka dikatakan sequency, atau Walsh.dipesan. Walsh fungsi pada waktu t dan dari
sequency n ditunjuk WAL (n. t). Pemeriksaan
Gambar 2.6 menunjukkan bahwa ada jumlah yang sama genap dan ganjil fungsi
Walsh, hanya karena ada yang sesuai cosinusoidal dan sinusoidal komponen seri
Fourier. Bahkan fungsi, WAL (2k, t). ditulis
CAL (k. r), dan fungsi aneh, WAL (2k + 1,
t), yang ditulis SAL (k, t), di mana k = 1. 2,
... .N /2
- 1.
3.8.3 Hadamard transform
The
Hadamard transform, atau Walsh-HadamSebuahrd mengubah. adalah
basically sama dengan mengubah Walsh, tetapi
dengan fungsi Walsh dan karena deretan transformasi matrix re-memerintahkan. Resultan matriks Hadamard
terdiri subarrays orde kedua matriks. The Hadamard matrix Haif agar 8 x 8 diberikan sebagai 8H pada Gambar 3.7. dan dapat
dilihat untuk conssayast matriks
Matriks Hadamard
pesanan 2N dapat diperoleh secara rekursif dari 2H sebagai
Gambar
3.7 8 x 8 Hadamard matriks transformasi.
Nilai
properti rekursif ini adalah bahwa dengan Hadamard memesan fungsi Walsh
resultan cepat Walsh-Hadamard transformasi dapat lebih cepat dihitung dari DWT
tersebut. Hadamard-memerintahkan (atau secara alami memerintahkan) fungsi Walsh
adalahshown pada Gambar 3.8. Urutan Hadamard-pemesanan diperoleh dari urutan
Walsh-diperintahkan oleh
1)
mengekspresikan
urutan fungsi Walsh-memerintahkan dalam biner,
2)
bit-membalik
nilai biner.
3)
mengkonversi
nilai-nilai biner ke Gray kode, dan
4)
mengkonversi
nilai ini ke desimal.
3.8.4
Wavelet Transform
Dalam fisika Prinsip Ketidakpastian Heisenberg menyatakan bahwa tidak mungkin untuk secara bersamaan tahu kedua posisi x, dan momentum p, dari sebuah partikel dengan presisi. Faktanya :
Di mana h adalah konstanta Planck. Dengan bantuan persamaan Einstein,E = MR2, Prinsip ini dapat diterjemahkan ke domain dari pemrosesan sinyal untuk menyatakan waktu itu dan frekuensi tidak dapat diselesaikan secara bersamaan untuk presisi apapun. Demikian,
dimana dan mewakili resolusi frekuensi dan waktu. Jika T sangat diselesaikan, frekuensi akan kurang akurat, dan sebaliknya. Oleh karena itu dapat menjadi sulit untuk simultancously ukuran untuk tingkat yang diperlukan akurasi frekuensi komponen sinyal dan waktu di mana komponen terjadi, atau tekad tho dalam waktu komponen frekuensi yang berbeda. Ini bisa menjadi kasus untuk sinyal yang mengandung komponen frekuensi tinggi dari durasi pendek yang terjadi berdekatan dalam waktu bersama dengan komponen durasi yang lebih lama berjarak dekat di frekuensi dan terjadi pada waktu yang berbeda. sinyal tersebut adalah non-periodik. waveler transformasi alamat masalah umum ini mempengaruhi waktu - analisis frekuensi, dan menyediakan sarana untuk menganalisis non - sinyal stasioner. Transformasi wavelet sedap memiliki aplikasi untuk sinyal filtering.
3.8.5 Analisis Multiresolusi Dengan Metode Wavelet
Analisis
multiresolusi (MRA) mengacu pada partisi komponen sinyal ke sejumlah band
frekuensi. Ini dapat diimplementasikan menggunakan low pass filter dan tinggi
dan sub - sampling. Prosedur terbalik juga mungkin, yang memungkinkan
rekonstruksi sinyal. MRA dapat dilakukan dengan bantuan dari transformasi
wavelet diskrit menggunakan sinyal smapled. Telah digunakan dalam analisis isi
informasi dari gambar (Mallat, 1989) dan untuk menganalisis potensi
membangkitkan dari
Gambar 3.10 MRA
dekomposisi sinyal menggunakan metode wavelet
electroencephalogram
(Thakor et al, 1993), Mallta (1989) menghadirkan versi wavelet dari MRA dan
menjelaskan bagaimana untuk menerapkannya.
3.8.6 Representasi Sinyal Dengan Singularitas:
Transformasi Wavelet Metode
Telah
terbukti (Mallar dan Hwang 1992) bahwa semua sinyal dan kebisingan dapat
te-benar diwakili oleh singularitas mereka. Singularitas didefinisikan adalah
ayam dari eksponen Lipschitz mereka, Ini beberapa fungsi F (t) adalah
continucusly terdiferensiasi ar fo itu saya non-tunggal dan dikatakan Lipichit
1 Sinyal yang ane sot Lipachie 1 singulst dan digambarkan sebagai Lipschitz
awhare Hal ini juga posssble untuk hase eksponen ipsehitz nepalive. The
Limehitz esponcots mencirikan sinjulanities oleh besarnya dan IPI Dengan
descrihing nignals dalam hal sngufanities mereka dan thes emoving singufarities
yang tidak diinginkan fitlhered versi sinyal CNH rocontructed dari singularitas
yang tersisa. Teknik ini memiliki appplications di misalnya deteksi tepi dalam
gambar (Mallat dan Hwang 1992.) dan sigrsal denoining (Mallat sebuah Hwang
1992. Thang dan Zheng.:
Pertama
mempertimbangkan sinyal yang transformasi wavelet modulus maxima kebohongan
dalam membuat. di mana C adalah setiap konstan. kerucut seperti ditunjukkan
pada Gambar 8 x 1. Sekarang perhatikan maxima mereka dalam kerucut yang
terletak pada cennected kurva hetween scules diflerent, Sucth kurva dikenal
sebagai garis maksimum. Kemudian transformasi wavelet, Wia, T, terkait dengan
modulas maxima pada sach li maximam bervariasi dengan skala,, seperti
Oleh
karena itu, sebagai meningkatkan modulus wavelet transform incteascx. Dengan
kata lain increse modulus ou lewat untuk seales frekuensi yang lebih rendah.
Dengan demikian, mereka conient energi sinyal meningkat pada frekuensi yang
lebih rendah atau ekuivalen decreses di highes requencies. Dengan mengambil
logaritma dari Persamaan 3,8K, Equaticn 3,89 diperoleh
Kreta
mengubah ncy 2, skala rendah biggh froquency Modulus ansociated dengan noine 1
Moiali swociatad wh besarbesaran Sebuah garis maksimum
Gambar
3.13
Plot transformasi wavelet maksim, Wa, t), terhadap waktu untuk skala difterent
Ini
berarti bahwa, eksponen Lipschitz, adalah kemiringan maksimum sekutu
logarithmic- icaled garis lurus dari Persamaan 3.89 yang tetap berada di atas log | W (a, π) |. Ini akan segera terlihat menjadi berguna.
Modulus
maxima dari sinyal bising diilustrasikan murni skematis ian Gambar 3.13, yang
belum ditarik ke scufe Hal ini terlihat bahwa sinyal maxima st peningkatan
lokasi tertentu di magnitide pada skala yang lebih tinggi frequeneles lebih
rendah), sedangkan nouse noine maxima peningkatan magtitude pada skala yang
lebih rendah lebih tinggi frequenicies) dan juga meningkat jumlahnya. Umumnya,
sebagai skala dibelah dua, yang nomber dari tese naxima di dua kali lipat. LTU,
oleh sbuerving perubahan maxima di povitions sama dari skala untuk skala adalah
mungkin untuk mengidentifikasi mereka maxima terkait dengan e ini mungkin
Maxima karena itu dihapus dan tidak digunakan dalam rekonstruksi sinyal
denoised
Teknik
ini (Mallat dan Hwang. 199, Zhang dan Zseng, 1997) diaplikasikan pada ERP
simulasi di EEG data Bagian 3.8.5, The denoised dan ERP benar percobaan tunggal
ditunjukkan pada Gambar 3.14 untuk sinyal-to- rasio kebisingan -5,3 dB. Ini
merupakan sinyal-to-ketenangan besar ratin dibandingkan dengan -15 dB, yaitu
sekitar terbesar untuk menjadi
Diharapkan,
dan diekstraksi CNV tidak seperti CNV benar. Kenapa ini? Metode deteksi
singularitas didasarkan pada asumsi white noise dan sinyal EEG tidak putih, IE
simulasi diulang menggunakan white noise bukan EEG, maka hasil seperti pada
Gambar 3.15 diperoleh. Kali ini diekstrak CNV jauh lebih mirip dengan yang
benar oleh karena itu penting bahwa untuk metode untuk bekerja memuaskan
kebisingan harus putih.
Masalah
muncul ketika lokasi sinyal dan kebisingan maxima bersamaan. Jika maksimum
tidak dihapus, maka suara akan disimpan dalam sinyal. Jika maksimum dihapus,
beberapa sinyal akan dihapus, mengakibatkan distorsi dari sinyal
direkonstruksi. Sebuah solusi untuk ini adalah untuk mencari skala tinggi di
mana signa dominan trelatively besar rasio signal-to-noise) dan menerapkan
Persamaan 3.89 dalam kerucut, | (t - ta) | ≤ Ca, untuk menentukan e. Kemudian
rasio modulus maxima st locarions yang sama di seales menara yang berdekatan
dalam datang adalah 2" , karena itu besaran tue dari maxima di ini lebih
rendah skala muy dihitung dan digunakan dalam tecopstrikiim ignal Tentu saja
kerucut |.. ( t - ta) | ≤ Ca, dapat ditarik untuk setiap modilus maksimal.
Keterbatasan
lain dari denoising ini techqiues terletak pada accuruy mana modulas maxima
dari kebisingan dapat diidentifikasi dan dihapus. Hal ini tergantung pada te
presisi yang mungkin ditentukan yang akan tergantung pada wavelet lain yang
dipilih dan pada algoritma singularitas (modulus maksimum) dihapus, dan pada
algoritma reconstriction.
3.9 Sebuah aplikasi dari DCT: kompresi gambar
Gambar
3.16 adalah diagram blok dasar sistem kompresi JPEG untuk transmisi. Sebuah
sywtem terbalik diperlukan untuk rexeption dan dekompresi & dimensi DCT dua
dari data gambar pertama dihitung. DCT coefticients kemudian dikuantisasi dan
pengambangan yang berurutan nol-frekuensi atau DC koefisien kemudian
differentially kode pulsa termodulasi, dan aliran bit yang dihasilkan baik
Hutfman kode atau deret hitung kode yang coefficienis frekuensi lain (AC
koefisien) yang Huffman kode atau deret hitung kode. berjalan panjang dari nol
dijalankan panjang kode. Dua aliran data terkompresi yang dihasilkan terdiri dari
kode DC dan AC coefticients.
3.9.1 Discrete Cosine Transform
Setiap
gambar persegi panjang direpresentasikan sebagai array nilai numerik yang
menunjukkan atribut citra intensitas, nada, dan warna dalam beberapa cara.
Lihat, misalnya Pennehaker dan Mitchcell (1993) untuk rincian lebih lanjut.
Masing-masing dari nilai-nilai ini dikenal sebagai elemen gambar atau pixel,
dan seperti yang telah kita lihat, ada kemungkinan menjadi sejumlah besar dari
mereka dalam sebuah gambar. The statisties gambar dalam daerah diffenent
mungkin sangat berbeda, dan karena itu lebih baik untuk membagi gambar menjadi
beberapa blok yang lebih kecil bersebelahan charicteristis statistik yang lebih
serupa untuk trinsformation. blok yang lebih kecil juga menghasilkan kompresi
yang lebih tinggi karena korelasi tinggi antara piksel adjscent. Selanjutnya
transfoms dari hlocks smailler lebih mudah dihitung. Dengan demikian blok dasar
dalam standar IPEG terdiri dari persegi 8 x8 piksel,
Ini
8 x 8 blok pixel dua dimensi (2D), dan sehingga DCT 2D sesuai blok. Hal ini
dicapai dengan terlebih dahulu menghitung DCT setiap baris horizontal piksel,
menggantikan baris horizontal piksel dengan komponen DCT DCT horisontal
menghitung DCTs kolom, dan kemudian menggantikan masing-masing kolom dengan DCT
tthe DCT vertikal). Karena frekuensi komponen peningkatan DCTs horizomal dari
kiri ke kanan, dan orang-orang dari peningkatan DCTs vertikal dari atas ke
botom, resultan 2D DCT berisi frekuensi yang lebih rendah di bagian atas-lett
dan frekuensi yang lebih tinggi di bagian kanan bawah nya karena komponen
frekuensi yang lebih rendah sering amplitudo lebih besar dari componeta
frekuensi yang lebih tinggi, kiri atas MUP cenderung mengandung valucs relatif
besar dan bagian kanan nilai bawah lebih kecil.
3.9.2
2D DCT Koefisien Kuantisasi
Masing-masing
dari 64 koefisien DCT, Sty, tn, kini sepurately dikuantisasi ning quantizer
uniforn (lihat Bagian 2 42). Masing-masing dari 64 quantizens hos ukuran ste
yang berbeda masing-masing koefisien dinormalisasi dengan ukuran langkah
kuantisasi dari quanticer nya, dan hasil dibulatkan ke bilangan bulat terdekat.
Prosedur ini menciptakan sebuah array bilangan bulat berisi beberapa angka nol,
terutama di bagian kanan bawah dari array.
3.9.3
Coding
Kedua
set koefisien sekarang kode (lihat Gambar 3.16), yang selanjutnya kompres data.
Dimana berjalan lagi dari nol terjadi ini dapat dikompresi menggunakan
run-length coding. Kode ini menunjukkan berapa banyak angka nol berurutan ada.
Di mana ini skr pada akhir zig-zag mengakhiri blok codeword digunakan.
Koefisien tersisa Huffman dikodekan dalam sistem sekuensial bascline atau
arithmetivally dikodekan dalam diperpanjang DCT schemies Kedua kode mengandung
codeword panjang variabel, di mana codeword paling umum yang terjadi adalah
terpendek. Hal ini akan mengurangi jumlah bit yang akan ditransmisikan atau
dengan kata lain meningkatkan tingkat kompresi. Dua ini
Gambar
3.17
2D DCT urut zig-zag
Kode
yang paling efisien dalam bahwa mereka mengirimkan informasi yang paling dengan
sedikitnya jumlah bit. Kode Huffman menggunakan set optimal yang dipilih dari
codeword yang berisi jumlah integer bit informasi. coding aritmatika digunakan
untuk mendapatkan sekitar 10% peningkatan kinerja kompresi. Ini adalah bentuk
satu-pass coding adaptif di mana codeword buku af menyesuaikan secara dinamis
kepada data yang dikodekan. Topik teori informasi dan coding, bagaimanapun, ure
luar cakupan buku ini.
3.10 Contoh Bekerja
Contoh 3.8
Pertama empat nilai tegangan sampel dari
sinyal bandwidth yang 10 Hz sampel di 125 Hz adalah (0,5, 1, 1. 0.5). Menunjukkan
bagaimana transformasi Fourier diskrit dari urutan ini dapat diperoleh dengan menggunakan
transformasi Fourier cepat, dan karenanya mendapatkan tran Fouriersbentuk data.
Larutan
The grafik aliran untuk FFT diberikan pada Gambar 2.9. Kita punya
X (O)= G (O) + W ~ H (O) = G (O) + H (O)
G (O)
= x (O) + wgx (2) = x (O) + x (2)
H
(O) = x (l) + wgx (3) = x (l) + x (3)
Gambar 3.18 grafik aliran dari FFT pada Contoh 3.8
Dan tidak pendekatan yang baik untuk menempatkan FT =
T DFT, sehingga
FT =
(0,024, -0,004 (1 + j). 0004 (-1+ j)
Latihan
Soal
3. 1
Hitung DFT dari urutan data {O, 1. 1, O} dan memeriksa validitas jawaban
Anda dengan menghitung IDFT nya.
3. 2
Turunkan
dimensi X (k) dan x ² (k) .Hence menghitung dan plot spektrum energi dari
urutan data {O, 1, 1, O} yang DFT dihitung sebagai solusi untuk Soal 2.8.
3. 3
Jika urutan {O, l, 1, O} Masalah 2,8
diwakili sampel digital yang diambil dari bentuk gelombang tegangan sampel pada
125 Hz, tambang deter- spektral energi kepadatan dan fase spektrum Fourier
transform dari urutan data.
3. 4
Gunakan properti waktu-pergeseran dari
DFT dan solusi untuk Soal 2.8 untuk memperoleh amplitudo dan fase spektrum dari
seri waktu {O, 0, 0, 0, 0, 1, 1, O} untuk data sampel di instants t = 0, 1, 2,
..., 7 m
3. 5
Menggunakan hasil Soal 2,9 untuk
memverifikasi teorema Parse- val untuk data {O, 1, 1,0}.
3. 6
Gunakan teorema korelasi untuk
menghitung korelasi melingkar dari urutan data yang {l, l, 0,1} dan {1,0,0,1}.
Plot fungsi korelasi terhadap jumlah lag, j.
3. 7
Terapkan teorema korelasi untuk
menghitung korelasi linear dari urutan data yang {1,1,0, l} dan {l, 0,0, l}.
Plot fungsi korelasi terhadap nomor lag dan membandingkan hasilnya dengan
solusi untuk Soal 2.13, mantan plaining perbedaan.
3. 8
Hitung DFT dari urutan data {O, 1, 1, O}
menggunakan penipisan-in-time algoritma FFT (Coo- ley-Tukey). Periksa jawaban
dengan yang dari Soal 2.8. Bandingkan bers NUM penambahan kompleks dan
perkalian dalam dua metode.
3. 9
Hitung IFFT dari jawaban Soal 2.15 untuk
memverifikasi bahwa urutan data {O, 1, 1,0} diperoleh.
3. 10
Hitung FFT dari urutan data {O, 0, 1, 1,
1, 1, 0, O} dan plot amplitudo dan fase spektrum. Periksa jawaban dengan cal-
culating IFFT untuk mendapatkan quence se- asli.
3. 11
Menulis program komputer untuk
menghitung FFT dan IFFT. Periksa FFT dengan menghitung DFTs dari urutan data
yang {O, 1, 1, O} dari Soal 2.8, dan {l, l, 0, l} dan {l, 0, 0, l} Soal 2.13.
Periksa IFFT dengan menghitung IDFTs dari urutan DFT.
3. 12
Gunakan program FFT untuk menghitung
DFTs 1024-titik bentuk gelombang dari Memang, banyak persoalan 2,5 dan 2,7.
Plot spektrum energi dan fase mereka dan membandingkan dengan plot diperoleh
solusi untuk Masalah 2,5 dan 2,7.
3. 13
Menggunakan 1024-point FFT menghitung
dan plot spektrum energi dari pulsa persegi panjang dari amplitudo 5 V dan
lebar r = 6 s. Membandingkan hasilnya dengan yang dari Soal 2.7.
3. 14
(1) Gunakan
konvolusi teorema (Persamaan 2,37) untuk mendapatkan konvolusi dari spektrum
dari dua pasang bentuk gelombang:
(a) vs = sin (2π x l00t)
dan pulsa unit ketinggian, vw, berpusat pada t = 0 dan lebar 2 s;
(b)
vs
= sin (2π
× l00t)
dan
vw
= cos (2π
x 0.25T) untuk 1 ≤ t ≤ 1s
0
di tempat
lain
(2) Ketika
komponen Fourier dari sinyal yang diperoleh dengan menggunakan DFT data sampel,
sampel dari sinyal panjang (N - l) T berlaku digunakan, di mana N adalah jumlah
data dan T adalah interval antara sampel. Sinyal dikatakan telah berjendela
oleh jendela data panjang (N - l) T. Spektrum dihitung kemudian diberikan oleh
lilitan dari spektrum sinyal oleh spektrum jendela. Jika dalam kasus bentuk
gelombang dari bagian (1), Vs mewakili sinyal dan Vw adalah data window,
mengomentari suitabilities relatif dari dua jendela data untuk menentukan
sampel sinyal.
3. 15 Hitung kosinus diskrit, diskrit Walsh,
dan diskrit Hadamard mengubah dari urutan data {Ol, -0,2, 0,3, -0,4, 0,5, 1,5,
2, 1,5, 0,5, -0,4, 0,3, -0,2, 0,1}. Dengan asumsi transformasi ini sedang
dibandingkan sehubungan dengan efisiensi kompresi data mereka dengan nilai
ambang batas dipilih sebelumnya dari 0,35, peringkat mereka di urutan
preferensi.
Masalah MATLAB
3. 1
(a) Gunakan
fungsi MATLAB yang tepat untuk menemukan dengan pendekatan langsung, koefisien
DFT berikut 8-titik diskrit-urutan waktu.
x
(n) = [4,2,1,4,6,3,5,2]
(b) Menemukan,
menggunakan fungsi MATLAB yang tepat, urutan waktu diskrit yang correspoints ke
DFT koefisien berikut: 27 + 0j
-4,12132 + 3,792893j
4 + j
0,12132 - 4,707107j
5 + 0j
0,12132 + 4,707107j
4 - j
-4,12132 - 3,792893j
3. 2
(a) Hitung,
menggunakan MATLAB 32-point FFT dari urutan diskrit-waktu yang diberikan oleh:
x
(n) = 1, n = 0,1, ... ..15
0,
n = 16, 17, ... ..3j
(b) Hitung,
menggunakan MATLAB, FFT 64-titik urutan data dalam (a).
(c) Bandingkan
hasil yang diperoleh pada bagian (a) dan (b).
3A Program
bahasa C untuk perhitungan DFT langsung
Program
bahasa C yang diberikan di sini mengevaluasi, langsung, DFT atau IDFT dari
urutan diskrit-waktu, x (n):
dimana
W = ej-2π/
N dan
N adalah panjang urutan. Urutan input, x (n), harus dalam bentuk kompleks (real
dan imajiner). Untuk urutan data real, bagian imajiner dari data diatur ke nol.
Fungsi utama, DFTD.c, tercantum dalam Program 3A.l, dan fungsi yang menghitung
DFT atau IDFT di Program 3A.2. Dua fungsi, read__data () dan save__data (),
diperlukan untuk membaca urutan input data dan untuk menyimpan data
ditransformasikan (Program 3A.3). Input data diadakan dalam file input,
coeff.dat, dan output disimpan dalam dftout.dat berkas.
3A.1 Program
Fungsi utama dftd.c untuk perhitungan berasal dari DFT.
/ * ..
.................................................................................... * /
/ * Program untuk menghitung OFT
koefisien secara langsung *
/
/ * 3 fungsi lainnya yang
digunakan *
/
/ * *
/
/ * EC lfeachor. Juli 1992 *
/
/ * ..
.................................................................................... * /
# include “Dsp1.h”
# include “dift.h”
main ()
{
extern npt
panjang;
extern int inv;
printf (
"pilih jenis transformasi \ n");
printf ( "\
n");
printf ( "0
untuk maju DFT \ n");
printf ( "1
untuk inverse DFT \ n");
scanf ( "%
d", & inv);
read__data (),
DFT ();
save__data ();
keluar();
}
# include “dft.c”
# include “rdata.c”
# include “sdata.c”
output
disimpan dalam dftout.dat berkas.
Contoh Uji 3A.1
Gunakan
program DFT langsung untuk menemukan koefisien DFT berikut 8-titik
diskrit-waktu berurutan:
x
(n) = {4, 2, 1, 4, 6, 3, 5, 2}
file
input data, dibuat dengan PC EDLIN (paling pengolah kata dapat digunakan untuk
tujuan ini) untuk masalah, memiliki format berikut:
8
4
0
2
0
1
0
4
0
6
0
3
0
50
20
Baris
pertama menentukan panjang urutan data.
DFT
dari data, menggunakan program, diberikan di bawah ini:
k
|
XR (k)
|
XI (k)
|
0
|
27.000000
|
0.000000
|
1
|
-4,121320
|
3.292893
|
2
|
4.000000
|
1.000000
|
3
|
0.121320
|
-4,707107
|
4
|
5.000000
|
-,000000
|
5
|
0.121320
|
4.707107
|
6
|
4.000000
|
-1,000000
|
7
|
-4,121320
|
-3,292893
|
3B Program
C untuk radix-2 penipisan-in-time FFT
Program
FFT yang diberikan di sini adalah implementasi bahasa C dari radix-2 FFT
penipisan-in-time (Cooley dan Tukey, 1965). Program ini mengevaluasi DFT atau
IDFT dari quence se diskrit-waktu sebagaimana didefinisikan dalam persamaan
2A.l. Program ini terdiri dari main fungsi, dftf.c, dan tiga fungsi: fft (),
read_data (), dan save__data().
Program 3B.l
Fungsi utama, dftf.c, untuk DFTs menggunakan FFT penipisan-in-time komputasi.
/ * ….................................................................................... *
/
/ * Program untuk menghitung OFT koefisien
menggunakan DIT FFT * /
/ * 3 fungsi lainnya yang digunakan *
/
/ * *
/
/ * EC lfeachor. Juli 1992 *
/
/ * *
/
/ * ..
.................................................................................... * /
# include
"dsp1 H"
# include
"dft.h"
utama()
{
extern npt
panjang;
extern int inv;
printf (
"pilih jenis transformasi \ n");
printf ( "\
n");
printf ( "0
untuk maju DFT \ n");
printf ( "1
untuk inverse DFT \ n");
scanf ( "%
d", & inv);
read__data ()
FFT ();
save__data ()
keluar;
}
# include "fft.c ";
# include "rdata.c ";
# include "sdata.c ";
3C DFT
dan FFT dengan MATLAB
Fungsi
kunci dalam MATLAB dan MATLAB Signal Processing Toolbox untuk melakukan DFT
satu dimensi dan FFT adalah dftmtx, FFT, dan ifft. toolbox juga certains fungsi
untuk melakukan transformasi kosinus diskrit dan FFT dua dimensi.
Fungsi
dftmtx mungkin digunakan untuk menghitung diskrit Fourier transform dari
sqeunce Data N-titik vektor x dengan menggunakan perintah berikut:
X
= x * dftmtx (N)
dftmtx
yang menghitung dan mengembalikan faktor bermalas sebagai matriks kompleks N ×
N. Ini kemudian dikalikan dengan urutan data, x, untuk menghasilkan
transformasi Fourier diskrit nya. Kebalikan DFT dapat diperoleh dengan
menggunakan perintah conj:
X = x *conj (dftmtx (N)) yN
Fungsi
fft menghitung DFT dari urutan data satu dimensi menggunakan radix-2 algoritma
FFT (jika panjang data adalah kekuatan 2) dan fungsi ifft digunakan untuk
mencari inverse DFT.
 |
| Allyza Nanda Purwari |
 |
| John Mari Ervian S. |
 |
| Nurul Kholifah |