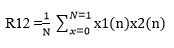Resume BAB 5 - Correlation and Convolution Kelompok 5
CORRELATION AND CONVOLUTION
5.1 Pengenalan
Pertimbangkan bagaimana dua urutan data, masing-masing terdiri dari nilai-nilai secara bersamaan sampel yang diambil dari dua bentuk gelombang yang sesuai, bisa dibandingkan. Jika dua bentuk gelombang bervariasi sama titik untuk titik, maka ukuran korelasi mereka mungkin diperoleh dengan mengambil jumlah dari produk dari pasangan merespon cor- poin. Usulan ini menjadi lebih meyakinkan ketika kasus dua urutan data independen dan acak dianggap. Dalam hal ini jumlah dari produk akan cenderung ke arah nomor acak makin kecil karena jumlah pasang poin meningkat. Hal ini karena semua nomor, positif dan negatif, sama-sama mungkin terjadi sehingga pasangan produk cenderung membatalkan diri pada penjumlahan. Sebaliknya, keberadaan sejumlah terbatas akan menunjukkan tingkat korelasi. Sebesar negatif akan menunjukkan korelasi negatif, yang merupakan peningkatan satu variabel berhubungan dengan penurunan variabel lain. The r12 korelasi silang (n) antara dua data yang sekuens x1 (n) dan x2 (n) masing-masing yang berisi data N mungkin karena itu ditulis sebagai
Definisi korelasi silang,bagaimanapun, menghasilkan hasil yang tergantung pada jumlah titik sampling yang diambil. Ini dikoreksi oleh normalisasi hasil untuk jumlah poin dengan membagi oleh N. alternatif ini dapat dianggap sebagai rata-rata jumlah produk. Dengan demikian, definisi ditingkatkan adalah
Perhitungan r12 diilustrasikan dalam contoh berikut, di mana angka-angka titik dalam urutan data n, dan urutan yang x1 dan x2.
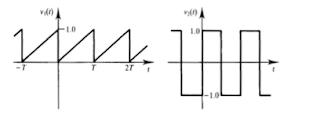
Namun, definisi ini kebutuhan modifikasi berguna. Dalam beberapa kasus mungkin menunjukkan korelasi nol meskipun dua bentuk gelombang yang 100% berkorelasi. Hal ini dapat terjadi misalnya ketika dua bentuk gelombang yang keluar dari fase, yang akan sering terjadi. Situasi ini digambarkan dengan bentuk gelombang dari Gambar 4.1. Dari angka ini terlihat bahwa setiap produk pasangan dalam korelasi adalah nol, dan karenanya korelasi adalah nol, karena salah satu baik x1 atau x2 selalu nol. Namun, bentuk gelombang yang jelas sangat berkorelasi, meskipun mereka keluar dari fase. Perbedaan fasa bisa, misalnya, terjadi karena x 1 adalah sinyal ence rujukan terbaik sementara x2 adalah output tertunda dari sirkuit. Untuk mengatasi perbedaan fase seperti itu perlu untuk menggeser, atau lag, salah satu bentuk gelombang sehubungan dengan lainnya. Biasanya x2 digeser ke kiri untuk menyelaraskan
Gambar 5.1 Keluar dari fase 100% bentuk gelombang berkorelasi dengan nol korelasi di lag nol.
Gambar 5.2 gelombang x2 = x1 + j bergeser j tertinggal di sebelah kiri gelombang x1.
bentuk gelombang sebelum korelasi. Seperti diilustrasikan dalam Gambar 4.2 ini setara dengan mengubah xi (n) untuk x2 (n + j), dimana j merupakan jumlah lag yang merupakan jumlah titik sampling dimana x2 telah bergeser ke kiri. Alternatif, tapi setara, prosedur adalah untuk menggeser x1 ke kanan. Rumus untuk korelasi silang demikian menjadi
Dalam prakteknya ketika dua bentuk gelombang berkorelasi hubungan fase mereka mungkin tidak akan diketahui dan korelasi akan dihitung untuk sejumlah kelambanan yang berbeda untuk membangun falue terbesar korelasi yang kemudian diambil menjadi nilai yang benar.
contoh 5.2
Pertimbangkan korelasi silang di atas dua urutan x1 (n) dan x2 (n) ata lag dari j = 3, yang menganggap r12 (3). Kedua urutan menjadi
Begitu
Tentu saja, itu juga mungkin untuk mempertimbangkan korelasi dalam domain waktu kontinu, dan beberapa analog sinyal korelasi diimplementasikan dengan cara ini. Dalam domain terus menerus n → t dan j → r dan
Namun, jika x1 (t) dan x2 (t) adalah periodik dengan periode T0 Persamaan 4.2 disederhanakan menjadi
Jika bentuk gelombang yang bentuk gelombang energi yang terbatas, misalnya nonperiodik jenis bentuk gelombang pulse- maka rata-rata dievaluasi selama waktu T sebagai T → ∞ tidak diambil karena kemudian l / T → 0 dan r12 (r) selalu makin kecil. Untuk kasus ini Persamaan 4.4 digunakan pada prinsipnya:
Dalam prakteknya, panjang record yang terbatas akan diproses dan Persamaan 4.5 atau 4.1 akan diterapkan:
Ada kesulitan lain yang berkaitan dengan lintas menghubungkan panjang terbatas data. Hal ini dapat dilihat dalam contoh di atas di mana r12 (3) = 2,667 ditentukan. Dalam contoh jumlah pasangan telah menurun 9-6 untuk lag tiga. Hasilnya adalah penurunan linear di r12 (j) sebagai j meningkat, menyebabkan diperdebatkan nilai-nilai r12 (j). Gambar 4. 3 menunjukkan bagaimana · RII (j) menurun dengan j murni sebagai akibat dari efek akhir, yaitu variasi yang sebenarnya di r12 (j) tidak termasuk.
Yang mana
Gambar 5.3 Pengaruh efek akhir pada r12 korelasi silang (j)
nilai-nilai dihitung dari korelasi silang karena itu mudah dikoreksi untuk efek akhir dengan menambahkan jr12 (0) / N dengan nilai-nilai r12 (j).
Nilai-nilai korelasi silang dihitung sesuai dengan rumus di atas tergantung pada nilai-nilai absolut dari data. Hal ini sering diperlukan untuk mengukur. cross-korelasi sesuai dengan skala tetap antara -1 dan + 1. Hal ini dapat dicapai dengan menormalkan nilai-nilai dengan jumlah yang tergantung pada kandungan energi dari data. Sebagai contoh, mempertimbangkan dua pasang bentuk gelombang x1 (n), x2 (n), dan x3 (n), x4 (n). Nilai data yang diberikan dalam tabel di bawah:
Seperti dapat dilihat dari Gambar 4.4, bentuk gelombang x1 (n) dan x3 (n) adalah sama, berbeda- ing hanya dalam besarnya. Hal yang sama berlaku dari pasangan x2 (n) dan x4 (n). Korelasi antara x1 (n) dan x2 (n) karena itu sama dengan bahwa antara x3 (n) dan x4 (n). Namun, cross-korelasi rn (l) dan R34 (1) adalah 1,47 dan 8,83 masing-masing. Mereka berbeda karena mereka bergantung pada nilai-nilai absolut dari data. Situasi ini dapat diperbaiki dengan normalisasi r12 korelasi silang (j) dengan faktor
dan juga untuk R34 (j). Ekspresi dinormalisasi untuk r12 (j) kemudian menjadi
p12 (j) dikenal sebagai koefisien korelasi silang. Nilainya selalu terletak tween be- -1 dan + 1. + 1 berarti 100% korelasi di
Gambar 5.4 Pasang bentuk gelombang {x1 (n), x2 (n)}, {x3 (n), x4 (n)} dari besaran yang berbeda tetapi sama lintas korelasi.
Nilai 0 berarti korelasi nol. Ini berarti sinyal benar-benar independen. Ini akan terjadi, misalnya, jika salah satu dari bentuk gelombang yang benar-benar acak. nilai-nilai kecil dari p12 (j) menunjukkan korelasi yang sangat rendah. Faktor normalisasi untuk r12 (j) dalam ilustrasi di atas adalah
dan untuk R34 (j) itu adalah
Karena itu
Dan
Sekarang p12 (1) = P34 (1) yang menunjukkan bahwa proses normalisasi ini memang memungkinkan perbandingan lintas-korelasi secara independen dari nilai data absolut.
Gambar Fungsi 5,5 Autokorelasi dari gelombang acak.
Sebuah kasus khusus terjadi ketika x1 (n) = x2 (n). gelombang tersebut kemudian silang · berkorelasi dengan dirinya sendiri. Proses ini dikenal sebagai autokorelasi. The auto · korelasi bentuk gelombang diberikan oleh
Fungsi autokorelasi memiliki satu properti yang sangat berguna dalam bahwa
di mana S adalah energi dinormalisasi dari bentuk gelombang. Ini menyediakan metode untuk menghitung energi dari sinyal.
5.2.1 silang dan autocorrelatio
Perawatan harus dilakukan ketika cross-menghubungkan dua urutan tidak sama panjang ketika mereka periodik. Hasil ini tidak mewakili periodisitas penuh urutan lagi dan, karena itu, tidak benar. Hal ini dapat ditunjukkan oleh lintas menghubungkan urutan a = {4, 3, 1, 6} dan b = {5, 2, 3} untuk mendapatkan rab (j).
Ini terlihat membutuhkan 6 lag sebelum b urutan mengulangi. Urutan panjang 4 dan 3 dan jumlah tertinggal diperlukan adalah 4 + 3 - 1 = 6. Ini mengungkapkan aturan umum untuk memperoleh linear korelasi silang dari dua sekuens ODIC peri dari panjang N 1 dan N 2: tambahkan menambah nol untuk setiap urutan untuk membuat panjang setiap urutan N 1 + N 2 - 1. ini dapat dinyatakan sebagai menambahkan N 2 - 1 nol ke urutan panjang N 1 dan menambahkan N 1 - 1 nol ke urutan panjang N2 • ini sekarang menunjukkan untuk urutan a dan b yang diberikan:
Dengan demikian, linear yang diperlukan korelasi silang a dan b adalah
Sejauh ini, contoh korelasi silang diambil semuanya diasumsikan data digital, namun korelasi silang juga dapat dilakukan secara analitis ketika pressions mantan analitis dapat ditulis untuk bentuk gelombang, termasuk saat ini membutuhkan penempatannya sek- dari bentuk gelombang. Dalam prakteknya prosedur analitis memiliki setara dalam penggunaan sirkuit analog untuk efek korelasi silang. Sebuah contoh dari analisis korelasi silang berikut.
Sangat mudah untuk mengekspresikan bentuk gelombang analitis dengan membagi mereka menjadi beberapa bagian garis lurus. Hal ini hanya diperlukan untuk melakukan hal ini selama satu periode, T, dari bentuk gelombang karena r12 (r) akan periodik di r dengan periode
Gambar 5.6 Bentuk gelombang v1 (t) dan v2 (t) misalnya korelasi silang.
Gambar 5. 7 Bagian dari v2 (t) untuk e → r → T.
Gambar 5.8 Bagian dari vi (t) untuk T / 2 → r → T.
yang menunjukkan bahwa v1 (t) harus dikalikan dengan tiga bagian berturut-turut v2 (t) di mana v2 (t) memiliki nilai-nilai berturut-turut -1, 1, -1. Untuk T / 2≤ T≤ T, Gambar 4.8 berlaku di mana nilai-nilai berturut-turut dari himpunan v2 (t) telah berubah menjadi 1, -1, + 1. Ini berarti ada dua bagian untuk solusi yang harus cocok di T = T / 2. Mengacu pada Gambar 4.7, korelasi silang dibagi menjadi tiga tions sek- dengan batas-batas. Karenanya
Untuk T / 2 ≤ t untuk TT, dan mengacu pada Gambar 5.8, terlihat bahwa
Gambar 5,9 r12 (r) sebagai fungsi dari r.
Mengganti T = T / 2 ke Persamaan 4.9 dan 4.10 memberikan r12 (r) = 1/4 dalam kedua kasus, membenarkan bahwa dua fungsi sesuai dengan benar. Gambar 4.9 menunjukkan plot rn (r) terhadap r untuk 0 ≤ T ≤ T.
Pemeriksaan persamaan ini menunjukkan bahwa istilah kedua di braket -o ketika T - oo, jadi ketika T - = f. oo itu merupakan kesalahan. Cos (w T) jangka merupakan efek kesalahan periodik.
Cos (wT) jangka memberikan sedikit kesalahan ketika wT = [(2n + l) / 2] 1T. Karena nilai-nilai w = 2rr / TP dan besar Tare dicari, ini sesuai dengan
Dosa ( «ir) jangka adalah setidaknya ketika wr = MTT, di mana m adalah bilangan bulat. Karenanya,
Sekarang perlu untuk membuat beberapa asumsi yang wajar. Asumsikan tion menderita penyakit untuk Tis besar puas dengan n ~ 10. Kemudian T ~ nT p / 2, atau
Dari Persamaan 4.13, nilai yang diijinkan terbesar dari r untuk komponen frekuensi terendah (m = 1) memenuhi
Menggabungkan Persamaan 5.14 dan 5.15,
Ini berarti bahwa ketika berhubungan gelombang kesalahan karena panjang data yang terbatas dapat diminimalkan dengan
(1) memastikan bahwa T ~ ST P' di mana TP adalah komponen frekuensi terendah yang menarik, dan
(2) tumpang tindih data dengan tidak lebih dari 20% dari panjang mereka.
Jadi, misalnya, jika sinyal pidato telepon dengan bandwidth 300 Hz sampai 3,4 kHz dan sampel di 40 kHz berkorelasi, TP = 1/300 = 3,3 x 10-3 s. Yang paling diterima panjang data akan menjadi 5 x 3,3 x 10-3 s = 16,7 ms dan pergeseran korelasi terbesar akan 3,33 ms, atau 133 titik data. Gambar 4.10 menunjukkan plot p11 (j), koefisien autokorelasi ofa gelombang murni acak, misalnya white noise. Nilai yang diharapkan dari R11 (j) dapat
Gambar 5.10 Koefisien autokorelasi dari gelombang acak.
terbukti E [R11 (j)] = -1 / N (Chatfield, 1980), di mana N adalah jumlah titik data, dan varians adalah var [R11 (j)] = itu ». Nilai yang diharapkan dari -1 / N ditunjukkan pada gambar seperti batas kepercayaan 95% dari - l / N dan ± 2 / N 1/2.
Begitu
Jadi R11 (r) dipandang periodik dalam r dengan periode, T. Ini adalah properti berguna karena memungkinkan deteksi sinyal periodik dalam kebisingan sinyal-to-noise rasio kecil. Autocorrelating gelombang cenderung mengurangi kebisingan sementara pada saat yang sama mengembangkan fungsi autokorelasi periodik dari sinyal.
S (t) dan q (t) diasumsikan uncorreleated. Fungsi autokorelasi sampel dari v (t) adalah rw (j) yang diberikan oleh
Untuk lebih kecil N, istilah korelasi silang dalam Persamaan 5.19 dan th autokorelasi dari kebisingan cenderung menuju nol dengan meningkatnya lag j.
5.2.2 Aplikasi korelasi
Perhitungan kepadatan spektral energi dan kandungan energi dari gelombang
Hal ini dapat menunjukkan bahwa
(5.25)
mana GE (f) adalah kerapatan spektral energi gelombang, yaitu kepadatan spektral energi dan fungsi autokorelasi merupakan Fourier Transform pasangan. Hal lanjut dapat menunjukkan bahwa
Hal lanjut dapat menunjukkan bahwa
(5.26)
di mana E adalah energi total bentuk gelombang.
5.2.3 Korelasi Cepat
Perhitungan korelasi dapat dipercepat oleh exploting teorema korelasi, biasanya dinyatakan sebagai
Dimana Fd-1 menunjukkan Fourier diskrit invers transformasi. Pendekatan ini memerlukan perhitungan dua Fourier diskrit Transform (DFTs) dan satu terbalik DFT, masing-masing yang paling mudah dijalankan menggunakan algoritma FFT (lihat bab 3). Jika jumlah istilah dalam urutan cukup besar, itu lebih cepat untuk menggunakan metode FFT ini daripada untuk menghitung korelasi silang secara langsung.
Prof dari teorema korelasi
Mari x1 (l), x2 (r), dan x3 (n) menjadi urutan peridic panjang N, dan membiarkan DFTs mereka menjadi x1 (k), x2 (k), dan x3 (k) masing-masing, lebih jauh lagi, biarkan
contoh 5.6
Bekerja di luar korelasi silang dari dua sequnces x1 (n) dan x2 (n) di bawah dengan menerapkan korelasi theorm:
X1 (n) = {1,0,0,1}
X2 (n) = {} 0.5,1,1,0.5
Pertama menggunakan teorema korelasi, persamaan 5.77.x1 (k) ditemukan di bagian 3,5 menjadi
X1 (k) = 2,1 + j, 0,1-j
Dan sebagainya
X1 * (k) = 2,1-j, -, 1 + j
X2 (k) paling mudah diperoleh dengan menggunakan algoritma FFT diberikan dalam bagian 3.5 dengan demikian, dengan x0 = 0,5, x2 = 1, x1 = 1, dan x3 = 0,5
X21 (0) = x0 + x2 = 1,5
X21 (1) = x0 + x2 = -0,5
X22 (0) = x1 + x3 = 1,5
X22 (1) x1-x3 = 0,5
X11 (0) = X21 (0) + x22 (0) = 3
X11 (1) = X21 (1) + (- j) x22 (1) = - 0,5-j0.5
X11 (2) = X21 (0) -x22 (0) = 0
X11 (3) = X21 (1) - (- j) x22 (1) = - 0,5 + j0.5
Membawa nilai-nilai dari FFTs bersama-sama memberikan
X1 * (k) = 2,1-j, 0,1 + j
X2 (k) = 3, -0,5-j0,5,0, -0,5 + j0.5
Begitu,
X1 * (0) x2 (0) = 2x3 = 6
X1 (1) x2 (1) = (1 -j) (- 0.5 - j0.5) = - 1
X1 * (2) x2 (2) = 0 x 0 = 0
X1 * (3) x2 (3) = 0,5 (1 + j) (- 1 + j) = - 1
Demikian
[X1 * (k) x2 (k)] 6, -1,0, -1
Sekarang perlu untuk mengambil invers DFT (IDFT) ini. Seperti explaind dalam bagian 3.6, yang IDFT yang diperoleh akan mengubah tanda-tanda eksponen (dalam faktor-faktor pembobotan WN) dalam algoritma FFT di atas dan membagi hasilnya dengan N.hence, dan tanpa mengubah notasi dalam algoritma,
X21 (0) = x0 + x2 = 6
X21 (1) = x0 + x2 = 6
X22 (0) = x1 + x3 = -2
X22 (1) = x1 + x3 = 0
X11 (0) = X21 (0) + x22 (0) = 4
X11 (1) = X21 (1) + jx22 (1) = 6
X11 (2) = X21 (0) -x22 (0) = 8
X11 (3) = X21 (1) -jx22 (1) = 6
Komponen FD-1 [x1 * (k) x2 (k)] diperoleh dengan membagi nilai-nilai x11 (0), x11 (1) .x11 (2), dan x11 (3) dengan N = 4, sehingga
FD-1 [x1 * (k) x2 (k)] = 1,1.5,2, 1,5
Sekarang, dari persamaan 5.77,
r12 (j) = FD-1 [x1 * (k) x2 (k)] = {0,25, 0,375, 0,5, 0,375}
korelasi ini akan melingkar karena semua data yang periodik dengan N. periodik The korelasi silang r12 (j) dapat bekerja secara langsung menjadi
r12 (0) = (1x0.5 + 0 + 0 + 1 x0.5) /4=0.25
r12 (1) = (1x1 + 0 + 0 + 1 x0.5) /4=0.375
r12 (2) = (1x1 + 0 + 0 + 1 x 1) /4=0.5
r12 (3) = (1x0.5 + 0 + 0 + 1 x 1) /4=0.375
yang velue berikutnya, r12 (4), adalah 0,25, sama seperti r12 (0), dan urutan mengulangi berkala. Ini adalah korelasi melingkar, seperti yang dibahas dalam bagian 5.2.1, dan hasil ini setuju dengan yang diperoleh di atas menggunakan teorema korelasi. korelasi theoremcan digunakan untuk mendapatkan korelasi linier dengan menambahkan menambah angka nol untuk dua sequeces sebagai explaind dalam bagian 5.2.1. dengan demikian, jika urutan lenghts yang N1 untuk x1 (n) dan N2 untuk x2 (n), dari N2 - 1 nol ditambahkan ke x1 (n) dan N1- 1 nol ditambahkan ke x2 (n). Korelasi silang kemudian dihitung dengan menggunakan dua sekuens ini ditambah, metode ini mengevaluasi lintas korelasi dengan menggunakan teorema korelasi dan FFTs dikenal sebagai korelasi cepat.
perhitungan korelasi silang juga dapat dipercepat dengan menerapkan mereka secara rekursif, dan ini akan diilustrasikan untuk kasus zero lag.the korelasi silang nol lag dari dua sampel bentuk gelombang x1 (n) dan x2 (n) adalah
r12 (0) =
ini melibatkan perhitungan produk N, N - 1 jumlah dan satu divisi. Hal ini dapat mengisi waktu yang berlebihan dalam aplikasi on-line di mana pasangan nilai data baru tiba di perhitungan sampel rate.the telah diulang ketika pasangan data berikutnya tersedia.
nilai baru = nilai sebelumnya + (produk dari dua data baru) - (produk dari dua data yang pertama)
ini adalah dasar dari recuirsive algorithm.each korelasi silang sekarang hanya membutuhkan satu perkalian, satu pengurangan, satu tambahan, dan satu divisi, asalkan produk pasangan data disimpan. Untuk N - korelasi point, pendekatan rekursif memberikan nilai yang benar setelah N pertama - 1 poin telah dihitung.
New rata = sebelumnya rata-rata + (baru datum-datum frist)
Hal ini juga memungkinkan untuk menggabungkan mean tingkat pengurangan dan korelasi silang perhitungan dalam satu algoritma rekursif. Mempertimbangkan
X1 (k) = x1 (n)
Dan
X2 (k) = x2 (n)
Nilai fungsi korelasi silang dari k set N poin
r12 (k) = x1 (n) x2 (n)
ketika sarana telah dihapus nilai fungsi korelasi silang menjadi r012 (k) di mana
r012 (k) = [x1 (n) -x1 (k)] [x2 (n) -x2 (k)]
yang, pada ekspansi, menyederhanakan untuk
r012 (k) = r12 (k) - x1 (k) x2 (k)
menggabungkan equitions 5.80 dan 5.83 memberikan
r12 (k) = r12 (k - 1) + [x1 (k) x2 (k) - x1 (k - N) x2 (k - N)]
dari persamaan 5.81,
x1 (k) = x1 (k - N) + [x1 (k) - x1 (k - N)]
dan
x2 (k) = x2 (k - 1) + [x2 (k) - x2 (k - N)]
persamaan 5,86-5,89 merupakan algoritma reqursive yang menggabungkan subtaction dari mean dari data dengan perhitungan korelasi silang. Setiap requirs calculetion hanya tiga perkalian, empat subtractions, tiga penambahan, dan empat divisions.practitioners harus diperhatikan perawatan yang harus dilakukan dalam pilihan N ketika nilai rata-rata dari data yang bervariasi, atau hasil yang tidak akurat dapat diperoleh.
5.3 deskripsi Konvolusi
Konvolusi jangka menjelaskan, antara lain, bagaimana input ke sistem berinteraksi dengan sistem untuk menghasilkan output. Umumnya sistem output akan menjadi versi tertunda dan dilemahkan atau diperkuat input.
Pertimbangkan sekarang penerapan urutan impuls x (m) ke sistem, diterapkan pada pengambilan sampel instan m, mengacu pada angka 5,19 output di instan 0 adalah y (0) diberikan oleh
y (0) = h (0) x (0)
di m pengambilan sampel instan = 1 output akan diberikan oleh h (0) x (1), efek dari input x saat ini (1), ditambah efek h tertunda (1) x (0) dari input diterapkan pada pengambilan sampel instan m = 0.thus
y (1) = h (1) x (0) + h (0) x (1)
sama, output selanjutnya akan diberikan oleh
y (2) = h (2) x (0) + h (1) x (1) + h (0) x (2)
y (3) = h (3) x (0) + h (2) x (1) + h (1) x (2) + h (0) x (3)
y (n) = h (n) x (0) + h (n - 1) x (1) + ... + h (0) x (n)
output my hanya ditulis dengan cara ini sebagai jumlah linear dari efek input sebelumnya jika sistem adalah salah satu linear. Persamaan 5.90 menggambarkan output dari sistem linear orde pertama.
Pemeriksaan ekspresi di atas mengungkapkan bahwa output diperoleh dengan mengalikan urutan input dengan titik yang sesuai dari fungsi respon impuls waktu terbalik. Atau, karena persamaan 5.90 dapat sama baiknya ditulis sebagai
y (n) = h (0) x (n) + h (1) x (n - 1) + ... + h (n) x (0)
output dapat dianggap sebagai produk dari pasangan yang sesuai dari poin dalam fungsi respon impuls dengan masukan waktu-dibalik sequence.thus jumlah lilitan setara dengan korelasi silang dari satu squence oleh urutan kedua kalinya-terbalik. Sejauh konvolusi istilah telah diambil untuk menggambarkan hasil convolving bersama-sama respon impuls dari sistem dan input ke system.However, ide dapat diperpanjang untuk konvolusi dari dua set data dan istilah selanjutnya akan dipertimbangkan dalam arti yang lebih umum ini.
cross-menghubungkan data windowed pada gambar 5.20 (c) dan 5.20 (f), memberikan
y (1) = 3 x 1 4 x 2 + 1 x 3 + 2 x 4 = 22
sama, ditemukan bahwa
y (2) = 2 x 1 3 x 2 + 4 x 3 + 1 x 4 = 24
dan
y (3) = 1 x 1 2 x 2 + 3 x 3 + 4 x 4 = 30
dimana setelah urutan keluaran mengulangi siklis, urutan output ini ditunjukkan pada gambar 5.20 (g)
ketika wavefroms didefinisikan dengan baik matematis konvolusi dapat dilakukan analytically.by mempertimbangkan contoh yang serupa, dan juga menggambarkan langkah-langkah yang terlibat grafis, adalah mungkin untuk mendapatkan pemahaman adonan dari proses konvolusi.
· 2 ≤ t ≤ 3 dan ada lengkap tumpang tindih af h (t - Ʈ) dan x (Ʈ) (gambar 5.21 (g)). Selama ini berbagai t,
y (t) = 6
y (t) = 6 (t - t + 2) = 12, 2 ≤ t ≤ 3
· 3 ≤ t ≤ 5. Ini adalah jenis lain dari daerah tumpang tindih ditunjukkan pada gambar 5.21 (h):
y (t) = = 6 = 6 (5 - t) = 30 - 6t
· t> 5. Seperti yang terlihat pada gambar 5.21 (i) ini merupakan wilayah kedua tidak ada tumpang tindih, dan sehingga tidak ada kontribusi terhadap integral konvolusi.
Tahapan 2 sampai 4 sehingga masing-masing memberikan kontribusi untuk konvolusi integral, dengan integral konvolusi memiliki ekspresi yang berbeda untuk masing-masing ofthe tiga wilayah sesuai dengan tiga tahap, dengan rincian sebagai berikut:
0 <t ≤ 2 y (t) = 6t
2 ≤ t ≤ 3 y (t) = 12
3 ≤ t ≤ 5 y (t) 30 - 6t
Dari ungkapan ini y (t) dapat diplot terhadap t seperti pada gambar 5.22
pemeriksaan persamaan ini berfungsi sebagai pengingat bahwa konvolusi itu dilakukan dalam waktu. Ini dikenal sebagai konvolusi dalam waktu domain.it diketahui bahwa adalah domain frekuensi komponen output dari sistem di ƒ frekuensi Y (ƒ), yang diberikan oleh
Y (ƒ) = H (ƒ) X (ƒ)
Dimana H (ƒ) adalah fungsi respon frekuensi dari sistem di ƒ frekuensi, dan X (ƒ) adalah Fourier Transform dari input x (t). Hal ini juga dapat menunjukkan bahwa H (ƒ) dia Fourier transfrom dari h (t). Kebalikan Fourier Transform persamaan 5.101 adalah.
F-1 [Y (ƒ)] = y (t) = F-1 [H (ƒ) X (ƒ)]
Menyatukan persamaan 5.96 dan 5,102 showns yang
y (t) = h (t) = F-1 [H (ƒ) X (ƒ)]
dengan demikian, terlihat bahwa cnvolution dari dua bentuk gelombang dalam domain ime setara dengan Fourier trasnform kebalikan dari produk dari transformasi Fourier dari dua bentuk gelombang. Fakta ini berguna sering dinyatakan dalam bentuk singkatan yang konvolusi dalam domain waktu adalah setara dengan perkalian dalam domain frekuensi.
5.3.1 sifat konvolusi
1) hukum komutatif
X1 (t) x2 (t) = x2 (t) x1 (t)
Catatan bahwa ini adalah identik dengan
x1 (τ) x2 (t - τ) dτ = x2 (τ) x1 (t - τ) dτ
2) hukum distributif
X1 (t) [x2 (t) + x3 (t)] = x1 (t) x2 (t) + x1 (t) x3 (t)
3) hukum asosiatif
X1 (t) [x2 (t) x3 (t)] = [x1 (t) x2 (t)] x3 (t)
Sifat-sifat ini dapat dibuktikan baik dengan memanipulasi integrasi yang terlibat atau dengan mempertimbangkan convolutions dalam hal lintas mengkorelasikan satu urutan dengan urutan kedua kalinya-terbalik.
5.3.2 konvolusi Edaran
Bagian 5.2.1 digambarkan bahwa hasil menghubungkan dua sekuens periodik leghth yang tidak sama adalah urutan siklik dari periode sama dengan yang dari urutan pendek, yang, oleh karena itu, hasil yang salah. Karena konvolusi setara dengan korelasi silang dari satu urutan dengan kebalikan dari urutan kedua, sama akan berlaku dari konvolusi. Oleh karena itu, seperti dengan korelasi, di lilit perlu bahwa dua urutan menjadi yang sama panjang.
Identifikasi 5.3.3 Sistem
Persamaan 5.95 memberikan hubungan antara input ke sistem, x (n), dan output, y (n). Istilah sistem identifikasi mengacu pada dtermination dari h (n) ketika tidak diketahui. Jika x sinyal uji (n) diterapkan dan y (n) diukur, h (n) dapat ditemukan sebagai berikut, selain dari metode yang dibahas dalam bagian 5.2.2.4 ,.
Persamaan 5.91 menyatakan bahwa y (n) = h (0) x (n) + h (1) x (n - 1) + ... + h (n) x (0). Ketika n = 0, y (0) = h (0) x (0), sehingga
sekarang, memperluas dan menata ulang 5,93 memberikan
begitu
persamaan 5,108 dan 5,110 memungkinkan h (n) harus dihitung.
contoh 5.8 tes sinyal, x (n) = {1, 1, 1}, diterapkan sistem dengan respon impuls yang tidak diketahui, h (n) .suatu keluaran sistem yang diamati adalah y (n) = {1, 4, 8, 10, 8, 4, 1). Tentukan h (n).
5.3.4 Pancar
Jika respon impuls dan output dari sistem diketahui, maka prosedur untuk memperoleh masukan yang tidak diketahui disebut sebagai dekonvolusi dapat dicapai dengan prosedur yang sama dengan yang dijelaskan di sectioen 5.3.3 pada identifikasi sistem.
5.3.5 dekonvolusi Blind
proses penentuan sinyal input dari sinyal output ketika respon impuls dari sistem tidak diketahui dikenal sebagai dekonvolusi buta. Sebuah metode untuk mencapai ini dijelaskan berdasarkan pengembangan Bell dan Sejnowski (1995). Masalah dan solusinya diilustrasikan pada Gambar 5.23, pada gambar 5.23 (a) diperlukan sinyal sumber yang tidak diketahui, x (n), dilewatkan melalui sistem respon impuls, h (n), untuk menghasilkan sinyal ouput terukur, ƒ (n). Ƒ (n) merupakan hasil konvolusi dari h (n) dengan x (n), h (n) x (n), dengan demikian terdistorsi oleh versi tertunda dari x (n).
disusun oleh :
 |
| Atikah Az Zahra |
 |
| Rizky putri Nurlaili |
 |
| Anugrah Satria |