7.7 Metode Frekuensi Sampling

Metode sampling frekuensi memungkinkan kita untuk merancang nonrecursive FIR filter untuk frekuensi standar selektif filter (lowpass, highpass, bandpass filter) dan filter dengan respon frekuensi yang berubah-ubah. Daya tarik unik metode sampling frekuensi adalah bahwa hal itu juga memungkinkan pelaksanaan rekursif FIR filter, mengarah ke mesin efisien filter. Dengan beberapa pembatasan, rekursif FIR filter koefisien yang adalah bilangan bulat sederhana dapat dirancang, yang menarik ketika hanya operasi aritmetika primitif yang memungkinkan, seperti dalam sistem yang dilaksanakan dengan standar mikroprosesor.

7.7.1 Nonrecursive Frekuensi Sampling Filter

Misal kita ingin memperoleh koefisien FIR filter respon frekuensi yang digambarkan dalam gambar 7.16(a). Kita dapat memulai dengan mengambil sampel N respon frekuensi interval . H(n) koefisien filter dapat diperoleh sebagai invers DFT sampel frekuensi:

Dimana adalah contoh ideal atau target respon frekuensi.

Gambar 7.16 Konsep frekuensi sampling. (a) respon frekuensi penyaring ideal lowpass. (b) sampel filter ideal lowpass. (c) frekuensi respon filter lowpass yang berasal dari sampel frekuensi (b).

Dapat ditunjukkan (Lihat contoh 7,9) bahwa filter fase linier, dengan respon positif impuls simetris, kita dapat menulis (untuk N genap),

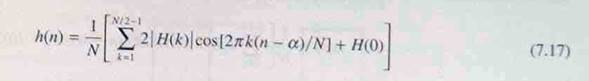
Dimana . N ganjil, batas atas kesimpulannya adalah (N-1) / 2. Filter dihasilkan akan memiliki respon frekuensi yang tepat sama seperti respon asli di sampling instants. Namun, antara instants sampel, respons mungkin akan sangat berbeda (gambar 7.16(c)). Untuk mendapatkan baik digunakan untuk respon frekuensi yang diinginkan, dengan jelas kita harus mengambil jumlah frekuensi sampel yang memadai.

Frekuensi alternatif sampling filter, dikenal sebagai tipe 2, hasil jika kita mengambil sampel frekuensi interval

Gambar 7,17 membandingkan sampling grid untuk kedua jenis skema frekuensi sampling. Untuk spesifikasi filter tertentu, kedua metode akan mengakibatkan tanggapan frekuensi yang agak berbeda. Desainer perlu memutuskan mana dari dua jenis terbaik sesuai dengan kebutuhannya.

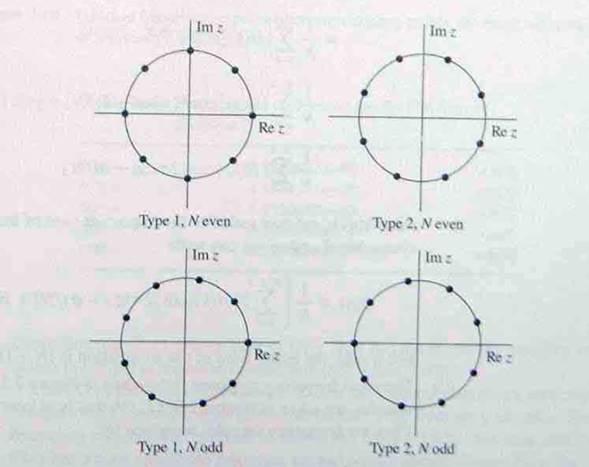
Gambar 7,17 Empat kemungkinan z-plane sampling grid untuk dua jenis frekuensi sampling filter.

7.7.1.1 Mengoptimalkan Respon Amplitudo

Untuk meningkatkan respon amplitudo frekuensi sampling filter, dengan mengorbankan transisi lebih luas, kita dapat memperkenalkan frekuensi sampel di band transisi. Gambar 7,19 menggambarkan sebuah spesifikasi yang khas untuk filter lowpass dengan tiga transisi band frekuensi sampel. Untuk lowpass filter, stopband redaman meningkat, sekitar 20 dB untuk setiap transisi band frekuensi sampel (Rabiner et al., 1970), dengan sebuah sesuai peningkatan lebar transisi:

stopband perkiraan atenuasi (25 + 20 M) dB

perkiraan transisi lebar (M + 1) F, / N

di mana M adalah jumlah transisi band frekuensi sampel dan N adalah panjang filter.

Nilai-nilai transisi band frekuensi sampel yang akan memberikan redaman yang optimal stopband ditentukan oleh proses optimasi (Rabiner et al., 1970). Tujuan berguna optimasi adalah untuk mencari nilai tangan transisi sampel frekuensi, yang meminimalkan puncak stopband riak (yaitu mereka memaksimalkan redaman stopband). Secara matematis, ini dapat dinyatakan sebagai:

Dimana adalah, masing-masing, tanggapan frekuensi ideal dan aktual dari filter, W adalah faktor bobot.

Rabiner et al. (1970) telah menyediakan tabel yang optimal (dalam arti Persamaan 7.22) nilai-nilai sampel pita frekuensi transisi yang banyak digunakan. Sampel dari nilai-nilai optimal dari sampel pita frekuensi transisi diberikan pada Tabel 7.11 untuk

Gambar 7.19 Sampel frekuensi filter lowpass termasuk tiga sampel pita transisi. Catatan: karena simetri dalam respons amplitudo hanya separuh respon filter yang ditampilkan.

Tabel 7.11 Sampel pita frekuensi transisi optimal untuk tipe 1 filter sampling frekuensi lowpass untuk N = 15.

BW mengacu pada jumlah sampel frekuensi dalam passband.

N = 15. Dalam tabel, bandwidth mengacu pada jumlah sampel frekuensi dalam passband filter.

Dalam kebanyakan kasus, nilai-nilai sampel frekuensi tangan transisi biasanya terletak pada rentang berikut: untuk satu sampel frekuensi transisi.

0.250 < T < 0.450

Untuk dua transisi sample frekuensi,

0.040<T1 <0.150

0.450 < T2 < 0.650

Untuk tiga transisi sampel frekuensi,

0.003 < T1 < 0.035

0.100 < T2 < 0.300

0.550 < <0.750

Nilai yang lebih rendah adalah untuk filter dengan lebar pita lebar dan menyebabkan lebih banyak redaman stopband.

7.7.1.2 Desain Otomatic dari Frekuensi Sampling

Tabel nilai-nilai optimal transisi band frekuensi sampel tersedia dalam literatur (Rabiner et di, 1970) dan secara luas digunakan untuk merancang frekuensi sampling filter. Jika perancang ingin filter tidak ditabulasikan, nilai-nilai perkiraan transisi band frekuensi sampel dapat diperoleh oleh interpolasi linier, tetapi hal ini tidak selalu mungkin, terutama jika desain melibatkan sejumlah besar transisi band sampel. Program komputer tujuan umum baru-baru ini telah dikembangkan untuk mengotomatisasi berbagai aspek dari desain nonrecursive dan rekursif frekuensi sampling filter (Ifeachor dan Harris, 1993: Harris dan lfeachor, 1998).

7.7.2 Rekursif Frekuensi Sampling Filter

Dapat ditunjukkan (Lihat contoh 7,12) bahwa fungsi transfer FIR filter H(z), dapat dinyatakan dalam bentuk rekursif:

Dimana

Masalah kestabilan dapat dihindari dengan sampling H(z) di radius, r sedikit kurang dari kesatuan. Dengan demikian fungsi transfer dalam hal ini menjadi

Untuk frekuensi standar fase linier selektif filter (dorongan simetris positif respon), dapat ditunjukkan (Lihat contoh 7,12) bahwa persamaan 7.24 dapat dinyatakan sebagai

di mana  dan untuk N genap M = N / 2-1. Diagram realisasi untuk Persamaan 7.25 digambarkan pada Gambar 7.22.

7.7.3 Filter Frekuensi Sampling Dengan Koefisien Sederhana

Pelaksanaan rekursif dari filter FIR greatle mengurangi jumlah operasi aritmatika dalam filter digital. Jika filter selain memiliki koefisien yang bilangan bulat sederhana

(Atau pangkat dari 2) efisiensi komputasi adalah greatle ditingkatkan, sehingga menarik dalam aplikasi di mana prosesor dengan operasi aritmatika primitif, seperti mikroprosesor biasa, digunakan. Lynn (1975) telah mengembangkan keluarga filter sampling frekuensi dengan koefisien bilangan bulat kecil.

Jelas bahwa penentuan fungsi transfer untuk frekuensi sampling dengan koefisien integer adalah proses yang sangat sederhana. Namun, respon amplitudo filter seperti itu sering buruk dan perancang dibatasi di mana paspor dapat ditemukan. Untuk meningkatkan karakteristik frekuensi atenuasi dan cutoff filter ini, transfer fuction dapat dinaikkan ke nilai integer (Lynn , 1973, 1975).

7.7.4 Ringkasan Metode Sampling Frekuensi

 Langkah 1 Tentukan respons frekuensi ideal atau yang diinginkan, atenuasi stopband dan frekuensi bandangan dari filter target.

 Langkah 2 dari spesifikasi pilih tipe 1 filter frekuensi sampling, mana frekuensi sampel yang diambil pada interval kF n, atau filter frekuensi sampling tipe 2, yang mana frekuensi sampel yang diambil pada interval (k + ½) F/N.

 Langkah 3 menggunakan spesifikasi dalam langkah 1 dan desain meja (Rabiner et al., 1970) untuk menentukan N, jumlah frekuensi sampel respon frekuensi yang ideal, M, jumlah transisi band frekuensi sampel, BW, jumlah frekuensi sampel di passband , dan T, nilai-nilai transisi band frekuensi sampel (saya = 1, 2,..., M).

 Langkah 4 menggunakan persamaan sesuai untuk menghitung koefisien filter.

Atau program berbasis komputer yang menggunakan algoritma genetik dapat digunakan untuk melaksanakan langkah 2 ke 4 (Harris dan Ifeachor, 1998).

7.8 Perbandingan Jendela, Optimal Dan Frekuensi Metode Sampling

Metode optimal menyediakan cara yang mudah dan efisien komputasi FIR filter koefisien. Untuk sebagian besar aplikasi metode optimal akan menghasilkan filter dengan baik amplitudo karakteristik respon untuk nilai-nilai yang masuk akal metode N.

Dengan tidak adanya perangkat lunak yang optimal atau ketika riak passband dan stopband sama, metode jendela mewakili pilihan yang baik. Ini adalah metode yang sangat sederhana untuk diterapkan dan secara konseptual mudah dimengerti. Namun, metode optimal akan sering memberikan solusi yang lebih ekonomis dalam hal jumlah koefisien filter. Metode window tidak memungkinkan desainer mengontrol secara tepat frekuensi cutoff atau riak di passband dan stopband.

Pendekatan sampling frekuensi adalah satu-satunya metode yang memungkinkan penerapan filter FIR non-rekursif dan rekursif, dan harus digunakan ketika implementasi seperti itu dibayangkan sebagai pendekatan rekursif yang ekonomis secara komputasi. Khusus dari dengan koefisien integer harus dipertimbangkan hanya ketika aritmatika primitif dan pemrograman dalam mikroprosesor standar), tetapi pemeriksaan harus selalu dilakukan untuk melihat apakah respon amplitudonya buruk dapat diterima.

Contoh 7.14

Dua filter FIR bandpass fase linier diperlukan untuk memenuhi spesifikasi berikut: untuk filter 1.

Passband 8-12 khz
stopband ripple 0.001
peak passband ripple 0.001
sampling frequency 44.14 kHz
transition width 3 kHz

Dan untuk filter 2,

passband 8-12 kHz
stopband riak 0,001
puncak riak passband 0,001
frekuensi sampling 44,14 kHz
lebar transisi 3 kHz

Memperoleh dan membandingkan respon frekuensi untuk masing-masing filter menggunakan

(1) Jendela metode,

(2) Metode pengambilan sampel frekuensi, dan

(3) Metode yang optimal

Solusi

(1) metode jendela Untuk filter 1, dari spesifikasi passband riak adalah 20 log (1 + 0,001) = 0,008 68 dB redaman stopband adalah -20 log (0,001) = 60 dB. Dari Persamaan 7.10 dan 7.11 parameter untuk jendela Kaiser adalah

frekuensi cutoff 6,5 kHz, 13,5 kHz

parameter riak, β 5,653

Jumlah koefisien filter 53

frekuensi sampling 44,14 kHz

Untuk filter 2, hasilnya adalah sama untuk filter saya karena dalam metode jendela passband dan stopband riak selalu kurang lebih sama.

Spektrum Filter yang dihasilkan diberikan pada Gambar 7.25 (a).

(2) metode sampling Freuency Untuk filter 1, kami mengasumsikan tipe 1 sampel filter, dan filter panjang, N, dipilih sebagai 53, sama seperti untuk metode jendela. Dari desain-tabel (Rabiner et al., 1970), kami menemukan bahwa kami memerlukan dua sampel frekuensi band transisi untuk mencapai redaman stopband yang diinginkan dari 60 dB, dengan Fs = 44,14 kHz, M = 2, N = 53. Sampling dari respon frekuensi yang ideal, untuk N = 53, memberikan

k = 0, 1, ...., 7

0,106 89 k = 8

0,592 53 k = 9

1 k = 10-14

0,592 53 k = 15

0,106 89 k = 16

0 k = 17-26

Menggunakan program fresamp.c (lihat lampiran), filter diperoleh dan respon frekuensi yang sesuai digambarkan pada Gambar 7,25 (b).

karena stopband pelemahan adalah sama untuk kedua filter, filter 2 adalah sama sebagai filter 1.

(3) Metode optik Untuk filter 1, dari spesifikasi frekuensi bandedge dinormalisasi adalah 0, 5 / 44,14, 8 / 44,14, 12 / 44,14, 15 / 44,14 dan 22,07 / 44,14, yaitu 0, 0,113 28, 0,181 24, 0,271 86, 0,339 83 dan 0,5. menggunakan program dalam lampiran, kita menemukan N = 49,6. karena kedua pass band dan stopband riak adalah sama, bobot di tiga band yang sama. Parameter input ke program desain yang optimal adalah

jumlah koefisien penyaring 49

frekuensi bandedge 0, 0,113 28, 0,181 24, 0,271 86, 0,339 83, 0,5

bobot 5, 5, 5

Parameter input untuk filter 2 adalah

jumlah koefisien penyaring 39 (39,45)

frekuensi bandedge 0, 0,113 28, 0,181 24, 0,271 86, 0,339 83, 0,5

bobot 10, 1, 10

tanggapan frekuensi yang dihasilkan untuk metode yang optimal ditunjukkan pada Gambar 7.25 (c) dan 7,25 (d).

7.9 FIR Khusus Topik Desain Filter

7.9.1 Filter FIR Half-Band

Half-band filter adalah jenis khusus dari filter FIR. Fitur menarik utama filter half-band adalah bahwa hampir setengah koefisien filter adalah nol yang mengarah ke pengurangan upaya komputasi dengan faktor 2. Fitur ini membuat setengah-band filter yang menarik dalam aplikasi seperti pengolahan multirate mana ada kebutuhan untuk efisien penyaringan anti-aliasing dan / atau penyaringan anti-image untuk mengubah sampling rate data.

filter half-band kausal dicirikan oleh fitur berikut:

(1) Passband dan stopband riak adalah sama, yaitu

(7.33)

(2) Passband dan stopband tepi frekuensi berhubungan dengan cara berikut:

(7.34)

(3) Respon frekuensi simetris sekitar seperempat dari frekuensi sampling. Artinya, di

(7.35)

Juga pada frekuensi ini, respon frekuensi dinormalisasi turun dengan faktor 2, yaitu:

(4) Dalam respon impuls satuan, untuk N aneh, setiap koefisien lainnya adalah nol kecuali:

(7.36)

0,5,

Koefisien dari filter setengah-band dapat diperoleh dengan menggunakan metode FIR dijelaskan ealier, seperti jendela dan metode yang optimal. Dalam menggunakan metode, kendala yang diberikan dalam Persamaan 7.33 dan 7.34 harus dikenakan.

Gambar 7.26 (A) Respon frekuensi dari setengah-band lowpass filter, (b) Frequencyresponse dari (i) filter lowpass ideal dan (ii) dan setara yang ideal penyaring highpass.

7.9.2 Transformasi Frekuensi

Sebuah hubungan yang sederhana ada antara lowpass dan highpass filter yang memungkinkan perubahan tersebut. Koefisien dari filter FIR highpass dapat trivial diperoleh dari orang-orang dari filter lowpass setara dengan mengubah tanda-tanda koefisien sebagai berikut:

(7.37)

Hubungan ini didasarkan pada pengetahuan bahwa respon frekuensi tinggi-pass filter adalah sama dengan filter lowpass tapi frekuensi diterjemahkan oleh setengah frekuensi sampling (lihat Gambar 7.26 (b)). Sehingga respon frekuensi highpass filter dapat diperoleh dari yang lowpass dengan mengganti f oleh Fs / 2-f:

(7.38)

7.9.3 Komputasi Filter FIR Efisien

Dalam sistem kontrol, misalnya, penggunaan filter seperti di dalam loop umpan balik dapat menyebabkan ketidakstabilan. Dalam kasus seperti filter fase minimum mungkin lebih tepat (lihat Taman dan Burrus, 1987).

Karakteristik equiripple dari metode yang optimal dapat menyebabkan gema dalam respon impuls dari filter yang mungkin merupakan efek yang tidak diinginkan.

Dalam aplikasi lain, seperti pengolahan gambar, jumlah operasi aritmatika ketika filter FIR standar yang digunakan mungkin terlalu besar. Sayangnya, koefisien bilangan bulat filter tidak cocok untuk aplikasi seperti itu karena lemah karakteristik respon amplitudo mereka.

Dasar dari metode ini adalah untuk kaskade dua atau lebih bagian penyaring SD seperti yang ditunjukkan pada Gambar 7.27. Setiap bagian dasar melibatkan hampir perkalian apapun.

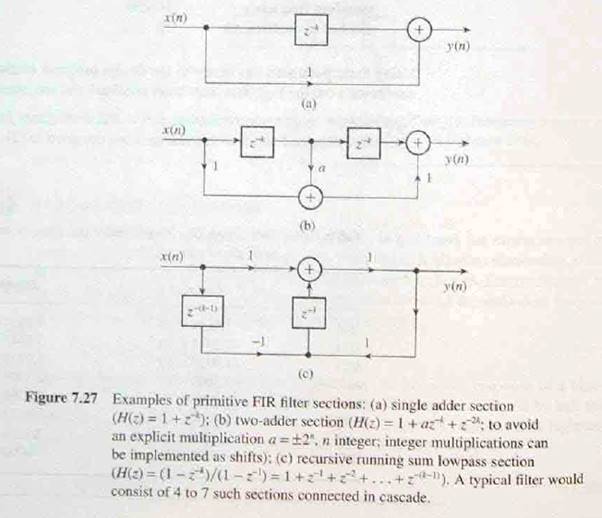
Masalah utama dengan metode ini termasuk sulitnya mencari cara yang efisien untuk memilih bagian penyaring SD kaskade dan fakta bahwa hanya filter dari urutan rendah dapat dirancang secara efisien. algoritma genetika telah digunakan untuk mengatasi masalah (Suckley, 1990).

7.10 Struktur Realisasi Untuk Filter FIR

FIR filter ditandai dengan fungsi transfer, H (z), yang diberikan oleh

struktur realisasi pada dasarnya memblokir (atau aliran) representasi diagram cara teoritis setara berbeda fungsi transfer bisa diatur. Dalam kebanyakan kasus, mereka terdiri dari interkoneksi pengganda, penambah / musim panas dan elemen delay. Ada banyak struktur realisasi FIR, tetapi hanya mereka yang umum digunakan disajikan di sini.

7.10.1 Struktur Transveral

The transversal (atau delay mengetuk) struktur digambarkan pada Gambar 7.28. Input, x (n), dan output, y (n), filter untuk struktur ini terkait hanya dengan

(7.39)

Dalam gambar, simbol z-1 merupakan penundaan satu sampel atau satuan waktu. Jadi x (n-1) adalah x (n) tertunda satu sampel. Dalam implementasi digital, kotak berlabel

Gambar 7.28 struktur filter transversal

z-1 bisa mewakili shift register atau lebih umum lokasi memori di RAM. Struktur transversal filter struktur FIR paling populer.

Sampel output, y (n), adalah jumlah tertimbang dari masukan ini, x (n), dan N-1 sampel sebelumnya input, yaitu x (n-1) ke x (NN). Untuk struktur transversal, perhitungan setiap sampel output, y (n), membutuhkan

§ N-1 lokasi memori untuk menyimpan N-1 sampel input,

§ lokasi memori N untuk menyimpan koefisien N,

§ N perkalian dan

§ N-1 penambahan.

7.10.2 Struktur Fase Linier

Sebuah variasi dari struktur transversal adalah struktur fase linier yang mengambil keuntungan dari simetri dalam koefisien respon impuls untuk filter fase FIR linear untuk mengurangi kompleksitas komputasi dari implementasi filter.

Untuk tipe 1 dan 2 filter fase linier, fungsi transfer dapat ditulis sebagai

Persamaan Perbedaan yang sesuai diberikan oleh

Perbandingan Persamaan 7.39 dan 7.41 menunjukkan bahwa struktur fase linear komputasi lebih efisien, membutuhkan sekitar setengah jumlah perkalian dan penambahan. Namun, di sebagian besar prosesor DSP Persamaan 7.39 mengarah ke implementasi yang lebih efisien, karena keuntungan komputasi dalam Persamaan 7.41 hilang dalam pengindeksan lebih kompleks data tersirat.

7.10.3 Struktur Lainnya

7.10.3.1 Konvolusi Cepat

Metode konvolusi cepat melibatkan pelaksanaan konvolusi operasi Persamaan 7.39 dalam domain frekuensi. Seperti yang telah dibahas dalam Bab 5, konvolusi dalam domain waktu sama dengan perkalian dalam domain frekuensi. Dalam istilah sederhana, penyaringan di sini dilakukan dengan terlebih dahulu menghitung DFTs dari x (n) dan h (n) (sesuai dengan zero padded), mengalikan ini bersama-sama dan kemudian memperoleh inverse mereka.

7.10.3.2 Struktur Frekuensi Sampling

Dalam struktur sampling frekuensi, filter dicirikan oleh sampel dari respon frekuensi yang dikehendaki, H (k), bukan koefisien respon impulsnya. Untuk filter narrowband, sebagian besar sampel frekuensi akan nol, sehingga filter sampling frekuensi yang dihasilkan akan memerlukan lebih sedikit koefisien dan karenanya perkalian dan penambahan daripada struktur transversal yang setara.

7.10.3.3 Struktur Transpose dan Kaskad

Struktur transpose mirip dengan struktur langsung, kecuali bahwa jumlah parsial masuk ke tahap berikutnya. Metode ini lebih rentan terhadap suara ronde daripada metode langsung. Dalam realisasi kaskade, fungsi transfer, H (z), dinyatakan sebagai produk bagian orde kedua dan orde pertama. Struktur transpose dan cascade jarang digunakan untuk filter FIR dalam implementasi DSP saat ini.

7.10.4 Memilih Di Antara Struktur

Struktur langsung sangat mudah untuk program dan efisien dilaksanakan oleh kebanyakan chip DSP yang ini memiliki petunjuk dirancang untuk traversal FIR penyaringan. Ini adalah struktur yang paling umum digunakan untuk menyadari nonrecursive filter dan daya tarik utama adalah kesederhanaan, memerlukan minimal komponen dan mengakses memori tidak rumit untuk data. Cascade kurang sensitif terhadap koefisien kesalahan dan kebisingan kuantisasi, tetapi coefficiemts memerlukan lebih banyak usaha untuk mendapatkan dan pemrograman tidak cocok dengan chip DSP arsitektur. Struktur cepat lilitan menawarkan komputasi keuntungan signifikan lebih dari yang lain, tetapi memerlukan ketersediaan FFT.

Struktur sampling frekuensi, untuk narrowband frekuensi selektif filter, mesin lebih efisien daripada struktur traversal setara. Untuk menghindari masalah stabilitas tiang dan nol struktur frekuensi sampling harus terletak sedikit di dalam unit lingkaran, misalnya di jari-jari r = 0.99. Struktur ini adalah pilihan yang alami ketika rekursif pelaksanaan FIR filter wajib. Struktur sangat modular dan cocok untuk pemrosesan paralel.

Secara umum, struktur tranversal harus digunakan kecuali persyaratan spesifikasi menentukan penggunaan struktur sampling frekuensi atau ada kebutuhan untuk menghitung spektrum data juga ketika konvolusi cepat harus digunakan.